《2025年学霸题中题八年级物理下册苏科版》

8. 核心素养科学探究(2024·南京秦淮区期末)
兴趣小组进行测固体颗粒密度的活动.
　　　　
(1) 小明选择天平和量筒完成实验:
①将天平放在水平台上，将游码移至“0”刻度线处，调节________直至天平平衡;
②如图1，测得颗粒的质量为________g;
③用量筒直接测量颗粒体积，会导致密度的测量值偏________.
(2) 小明调查发现工厂配有测量颗粒密度的密度秤，如图2，使用步骤如下:
　　　　
步骤1: 向容器B加入水，让水面升至容器的标记处，将空容器A与容器B一起放置在密度秤上，如图①，按下数据记忆键，记录密度秤上物体的总质量m₁;
步骤2: 将待测颗粒放入容器A，如图②，记录总质量m₂;
步骤3: 将容器B中的水倒去部分，将容器A中的待测颗粒全部倒入容器B中，如图③，再用胶头滴管向容器B中加入水，直到____________________，记录总质量m₃;
步骤4: 最后按下数据转换键，密度秤会根据程序设置的公式直接显示出待测颗粒的密度测量值，程序公式为ρ = __________（用ρ水及记录的物理量表示）.

答案：
(1)①平衡螺母　②74.2　③小　
(2)水面升至容器标记处　$\frac{m_{2} - m_{1}}{m_{2} - m_{3}}\rho_{水}$
解析:
(1)①根据天平使用规则，将天平放在水平台上，将游码移至“0”刻度线，调节平衡螺母，直到天平平衡；
②由图1可知，颗粒的质量为$m_{颗粒} = 50g + 20g + 4.2g = 74.2g$；
③由于量筒内的颗粒间存在空隙，使体积测量值偏大，由$\rho = \frac{m}{V}$可知密度会偏小。
(2)将容器B中的水倒去部分，将容器A中的待测颗粒全部倒入容器B中，如图③，再用胶头滴管向容器B中加入水，直到水面升至容器标记处，记录总质量$m_{3}$。由步骤①和②可知，颗粒的质量$m = m_{2} - m_{1}$，由步骤③和②相比，少了与颗粒同体积的水的质量，则颗粒排开水的质量$m_{水} = m_{2} - m_{3}$，由$\rho = \frac{m}{V}$知，颗粒的体积$V = V_{排水} = \frac{m_{水}}{\rho_{水}} = \frac{m_{2} - m_{3}}{\rho_{水}}$，则颗粒的密度$\rho = \frac{m}{V} = \frac{m_{2} - m_{1}}{\frac{m_{2} - m_{3}}{\rho_{水}}} = \frac{m_{2} - m_{1}}{m_{2} - m_{3}}\rho_{水}$。

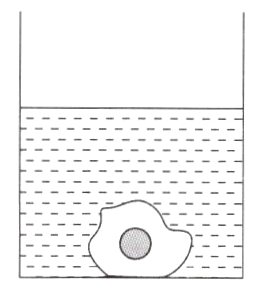
9. 如图所示，一只圆柱形容器质量为120g，底面积为100cm²，装满酒精时的总质量是280g;将其中含有一个小石头的冰块放入盛有一定水的该容器中，冰和石头的总质量是116g，冰块完全沉入水中，这时容器中的水面上升了1.1cm(未满)，当冰块的冰全部熔化后容器里的水面又下降了0.1cm(已知ρ冰 = 0.9×10³kg/m³，ρ酒精 = 0.8×10³kg/m³);求:
(1) 该容器的容积;
(2) 冰块中冰的质量;
(3) 石块的密度.
　　　　　　　　　　　　

答案：
(1)$200mL$　
(2)90g　
(3)$2.6g/cm^{3}$
解析:
(1)容器中酒精的质量为$m_{酒精} = 280g - 120g = 160g$，
由$\rho = \frac{m}{V}$可得容器的容积为$V = V_{酒精} = \frac{m_{酒精}}{\rho_{酒精}} = \frac{160g}{0.8g/cm^{3}} = 200cm^{3} = 200mL$。
(2)设整个冰块的体积为$V_{总}$，其中冰的体积为$V_{冰}$，石块的体积为$V_{石}$；冰和石块的总质量为$m_{总}$，其中冰的质量为$m_{冰}$，石块的质量为$m_{石}$；冰熔化成水后的水的质量为$m_{水} = m_{冰} = \rho_{冰}V_{冰}$，
冰熔化成水后的水的体积为$V_{水} = \frac{m_{水}}{\rho_{水}} = \frac{\rho_{冰}V_{冰}}{\rho_{水}}$。
由题知，冰熔化成水后减小的体积为$V_{冰} - V_{水} = V_{冰} - \frac{\rho_{冰}V_{冰}}{\rho_{水}} = S\Delta h_{2}$，
代入数据得$V_{冰} - \frac{0.9g/cm^{3}}{1.0g/cm^{3}}V_{冰} = 100cm^{2}×0.1cm$。
解得$V_{冰} = 100cm^{3}$。
冰的质量为$m_{冰} = \rho_{冰}V_{冰} = 0.9g/cm^{3}×100cm^{3} = 90g$。
(3)冰块中所含的石块质量为$m_{石} = m_{总} - m_{冰} = 116g - 90g = 26g$，
由题意可得，冰块和石块的总体积为$V_{总} = S\Delta h_{1} = 100cm^{2}×1.1cm = 110cm^{3}$，
石块的体积为$V_{石} = V_{总} - V_{冰} = 110cm^{3} - 100cm^{3} = 10cm^{3}$，
则石块的密度为$\rho_{石} = \frac{m_{石}}{V_{石}} = \frac{26g}{10cm^{3}} = 2.6g/cm^{3}$。