《2025年学霸题中题八年级物理下册苏科版》

12. 潜水艇在水舱内无水时应漂浮于海面，可以通过充入适量海水实现潜入海中.一潜水艇质量为3.3×10⁶ kg，海水密度为1.1×10³ kg/m³，g取10 N/kg.
（1）工程师对潜水艇进行试验，发现水舱内无水的潜水艇居然在海水中沉没，最终静止在水平船坞底部，如图甲所示，已知船坞底部对潜水艇的支持力为6.6×10⁵ N，求潜水艇的体积有多大？
（2）为了实现水舱内无水时潜水艇刚好悬浮在海水中，工程师先将潜水艇切割成两段，然后在这两段之间加入增补舱段，如图乙所示，建成潜水艇如图丙所示.已知增补舱段的质量为4.4×10⁴ kg，求增补舱段的体积有多大？
（3）在此基础上，工程师将潜水艇内的部分原设备更换为更________（填“轻”或“重”）的新设备，即可实现在水舱内无水时潜水艇漂浮于海面.
　　

答案：
(1)$2940m^{3}$
(2)$100m^{3}$
(3)轻
解析：本题考查阿基米德原理及物体的浮沉条件.
(1)潜水艇静止在水平船坞底部时，受到竖直向下的重力、竖直向上的支持力和浮力，三力平衡，则潜水艇受到的浮力为：$F_{浮}=G - F_{支}=mg - F_{支}=3.3\times10^{6}kg\times10N/kg - 6.6\times10^{5}N = 3.234\times10^{7}N$，根据阿基米德原理，潜水艇的体积为：$V=\frac{F_{浮}}{\rho_{海水}g}=\frac{3.234\times10^{7}N}{1.1\times10^{3}kg/m^{3}\times10N/kg}=2940m^{3}$.
(2)增加增补舱段后，潜水艇恰好悬浮在海水中. 由物体的浮沉条件可知，此时潜水艇的整体密度$\rho_{潜水艇}=\rho_{海水}=1.1\times10^{3}kg/m^{3}$，故可得：$\rho_{潜水艇}=\frac{m + m_{补}}{V + V_{补}}=\frac{3.3\times10^{6}kg + 4.4\times10^{4}kg}{2940m^{3}+V_{补}}=1.1\times10^{3}kg/m^{3}$，解得：$V_{补}=100m^{3}$.
(3)由于潜水艇内设备不影响潜水艇的整体体积，故不影响潜水艇在海水中受到的浮力. 根据物体的浮沉条件，要实现舱内无水时潜水艇漂浮于海面，需潜水艇重力小于浮力，故需减小潜水艇的总质量，故应将内部原设备更换为更轻的新设备.

13. （2024·无锡宜兴市期末）中国万米载人深潜器“奋斗者”号曾在马里亚纳海沟成功坐底，深度达10 909 m.图甲是“奋斗者”号，图乙是它的部分结构示意图.“奋斗者”号总质量为20 t，其底部装配有质量为2 t的可抛弃压载铁，中部安装有固体浮力材料，载人舱为空心球体.除载人舱及部分电路设施外，其余部分与海水相通.“奋斗者”号在海水中依靠改变自身重力和受到的海水浮力实现无动力下潜和上浮.忽略深潜器部件受到海水压力后的体积变化.(ρ海水=1.0×10³ kg/m³，g取10 N/kg)
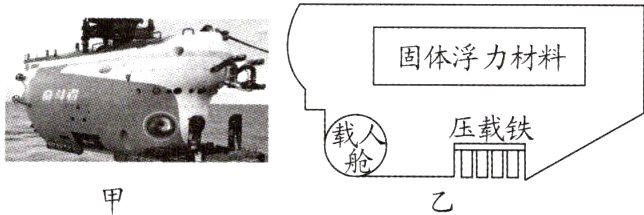
（1）若海水的密度均匀，“奋斗者”号在从海面下10 m匀速下潜至深度为10 000 m的过程中，所受海水的压强________，所受浮力________.（均填“变大”“变小”或“不变”）
（2）若固体浮力材料质量为2 400 kg，体积为4 m³.求：
①固体浮力材料的密度为多少？
②固体浮力材料完全浸没在海水中时，受到的浮力和自身重力之差为多少？
（3）“奋斗者”号完全浸没在海水中后匀速下潜，接近海沟底部时，抛掉部分压载铁后悬浮在海水中，待海底科研任务结束后，抛掉剩余的全部压载铁后匀速上浮至海面.若“奋斗者”号只在竖直方向实现下潜和上浮，船身与水平面平行，下潜和上浮过程中所受阻力大小不变，压载铁的密度为8.0×10³ kg/m³，则下潜和上浮过程中所受阻力为多少？
　

答案：
(1)变大 不变
(2)①$0.6\times10^{3}kg/m^{3}$ ②$1.6\times10^{4}N$
(3)$8.75\times10^{3}N$
解析：
(1)“奋斗者”号在从海面下 10 m 匀速下潜至深度为 10 000 m 的过程中，由$p = \rho gh$可知所受海水的压强变大，排开液体的体积不变，由$F_{浮}=\rho_{液}gV_{排}$可知所受浮力不变.
(2)①固体浮力材料的密度为$\rho=\frac{m}{V}=\frac{2400kg}{4m^{3}}=0.6\times10^{3}kg/m^{3}$.
②固体浮力材料完全浸没在海水中时，排开水的体积等于材料的体积，则此时受到的浮力为$F_{浮}=\rho_{海水}gV_{排}=\rho_{海水}gV = 1.0\times10^{3}kg/m^{3}\times10N/kg\times4m^{3}=4\times10^{4}N$. 材料的重力$G = mg = 2400kg\times10N/kg = 2.4\times10^{4}N$，受到的浮力和自身重力之差为$F_{浮}-G = 4\times10^{4}N - 2.4\times10^{4}N = 1.6\times10^{4}N$.
(3)已知“奋斗者”号总质量为 20 t，则总重力$G_{总}=m_{总}g = 20\times10^{3}kg\times10N/kg = 2\times10^{5}N$，质量为 2 t 的可抛弃压载铁的重力$G_{铁}=m_{铁}g = 2\times10^{3}kg\times10N/kg = 2\times10^{4}N$. 匀速下潜时$F_{浮}+F_{阻}=G_{总}\cdots$①，
抛掉 2 t 的压载铁，匀速上浮时，浮力$F_{浮}'=G_{总}-G_{铁}+F_{阻}\cdots$②，
由①②可得$F_{浮}+F_{浮}'=G_{总}+G_{总}-G_{铁}=3.8\times10^{5}N\cdots$③，
2 t 的压载铁的体积$V=\frac{m_{铁}}{\rho}=\frac{2\times10^{3}kg}{8.0\times10^{3}kg/m^{3}}=0.25m^{3}$，
由于压载铁浸没在水中，则$V_{铁}=V_{排}$，
则压载铁受到的浮力为$F_{1}=\rho_{水}gV = 1.0\times10^{3}kg/m^{3}\times10N/kg\times0.25m^{3}=2.5\times10^{3}N\cdots$④
匀速下潜和匀速上浮的浮力关系为$F_{浮}=F_{浮}'+F_{1}\cdots$⑤
由③④⑤可得$F_{浮}=1.9125\times10^{5}N$；由①可得下潜和上浮过程中所受阻力为$F_{阻}=G_{总}-F_{浮}=2\times10^{5}N - 1.9125\times10^{5}N = 8.75\times10^{3}N$.