第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
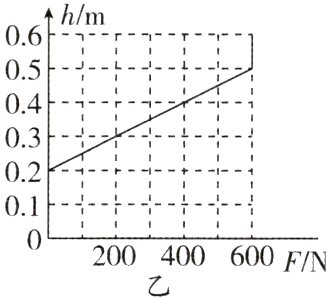
11. 为了给实心正方体工件表面均匀地涂上密度为0.8 g/cm³的某种油,需要用竖直向下的力F把漂浮在油面上的工件缓缓地压入油内,直到浸没油内,如图甲所示.收集有关数据并处理获得如图乙的图像,当F = 400 N时,工件的下底面与油面的距离h为________m,工件的质量为________kg,工件的密度为________g/cm³.(g取10 N/kg)



答案:
$0.4$ $40$ $0.32$ 解析:由图乙知道,$F$为$400\ N$时,工件的下底面与油面的距离$h$为$0.4\ m$. 当$F = 600\ N$时,工件刚好浸没在油中,且浸入油中的深度为$0.5\ m$,则工件的边长为$0.5\ m$,当$F = 0\ N$时,工件在油中处于漂浮状态,且$h_{浸} = 0.2\ m$,根据漂浮条件和阿基米德原理可得工件受到的重力$G = F_{浮} = \rho_{油}gV_{排} = \rho_{油}gL^{2}h_{浸} = 0.8\times10^{3}\ kg/m^{3}\times10\ N/kg\times(0.5\ m)^{2}\times0.2\ m = 400\ N$,由$G = mg$知道工件的质量$m = \frac{G}{g} = \frac{400\ N}{10\ N/kg} = 40\ kg$. 正方体工件的体积$V = (0.5\ m)^{3} = 0.125\ m^{3}$,则正方体工件的密度$\rho = \frac{m}{V} = \frac{40\ kg}{0.125\ m^{3}} = 0.32\times10^{3}\ kg/m^{3} = 0.32\ g/cm^{3}$.
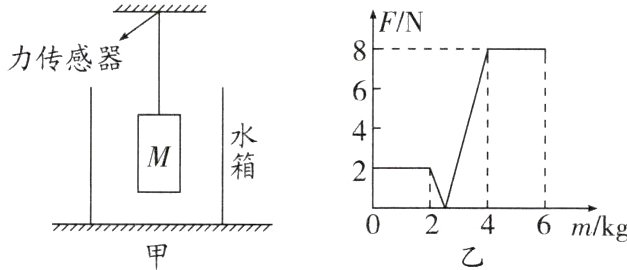
12. 核心素养 物理思维 如图甲所示为一个浮力感应装置,竖直细杆的上端通过力传感器连在天花板上,传感器可以显示出细杆的上端受到作用力的大小,下端与物体M相连,细杆及连接处的重力可忽略不计,向图甲所示的空水箱中加水直到刚好加满,图乙是力传感器的示数大小随水箱中加入水质量变化的图像.则物体M的重力为________N,浸没时受到的浮力为________N;当向容器中加水________kg时,传感器的示数为0 N.

答案:
$2$ $10$ $2.4$ 解析:由图乙可知,水箱中没有水时($m = 0$),力传感器受到的拉力$F_{1} = 2\ N$,则物体$M$的重力$G = F_{1} = 2\ N$. 由图乙可知,当$M$完全浸没时,力传感器的示数为$F_{2} = 8\ N>2\ N$,细杆对传感器的作用力为压力,故传感器对细杆有向下的作用力$F = F_{2} = 8\ N$,作用于物体$M$,此时物体$M$受到竖直向上的浮力、竖直向下的重力和杆的作用力,处于静止状态,则$M$受到的浮力$F_{浮} = G + F = 2\ N + 8\ N = 10\ N$. 综上可知,加水$2\ kg$时水面达到$M$的下表面(此时浮力为0),加水$4\ kg$时$M$刚好浸没(此时浮力为$10\ N$),该过程中增加水的质量为$2\ kg$,浮力增大了$10\ N$,所以每加$1\ kg$水,物体$M$受到的浮力增加$5\ N$;当传感器的示数为$0\ N$时,此时浮力等于$M$的重力,为$2\ N$,可得加水的质量为$m = 2\ kg + \frac{2\ N}{5\ N}\times1\ kg = 2.4\ kg$.
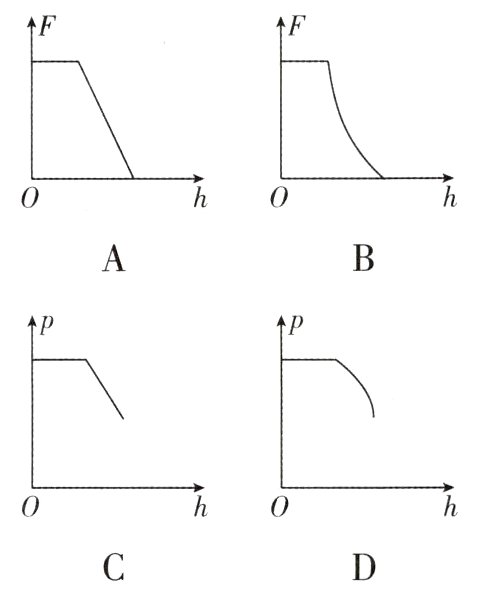
13. (2024·南通通州区期末)如图所示,圆柱形容器中盛有一定量的水,其中用细线吊有一个圆锥形金属块,顶端距水面有一小段距离.现向上提起金属块,直至离开水面.在此过程中,下列关于金属块所受浮力F、容器底部对桌面的压强p随金属块上升高度h变化的关系图线中,可能正确的是 ( )



答案:
D 解析:AB. 根据题意可知,在圆锥形金属块未露出水面之前,随着金属块上升高度的增大,其排开水的体积不变,根据$F_{浮} = \rho_{水}gV_{排}$可知,其受到的浮力不变,图像是一条平行于横轴的线段;当圆锥形金属块开始露出水面,直到完全露出水面的过程中,由于圆锥形金属块“上小下大”,因此随着金属块上升高度的增大,排开水的体积减小,且排开水的体积减小的幅度在变大,根据$F_{浮} = \rho_{水}gV_{排}$可知,金属块受到的浮力变小,且浮力变小的幅度在变大;金属块完全露出水面后,其排开水的体积为零,受到的浮力为零,故AB错误;CD. 把容器、水、金属块看成一个整体,那么整体受到容器、水、金属块的重力之和以及桌面对容器的支持力、向上的拉力作用,即$F_{支} + F_{拉} = G_{容} + G_{水} + G_{金属块}$,所以桌面对容器的支持力为$F_{支} = G_{容} + G_{水} + G_{金属块} - F_{拉} = G_{容} + G_{水} + F$,其中$F$为金属块受到的浮力,根据力的作用是相互的可知,容器对桌面的压力为$F_{压} = F_{支} = G_{容} + G_{水} + F$,则容器底部对桌面的压强为$p = \frac{F_{压}}{S} = \frac{G_{容} + G_{水} + F}{S}$. 容器的重力以及水的重力不变,容器的底面积不变,所以在金属块未完全露出水面之前,容器底部对桌面的压强$p$随金属块上升高度$h$变化的关系图线的大致趋势应与金属块所受浮力$F$随金属块上升高度$h$变化的关系图线相似,但金属块刚完全离开水面时,容器底部对桌面的压强不为零,故D正确,C错误. 故选D.
14. 有两个不吸水的圆柱体A和圆柱体B,A的顶部系有一根轻质细线,已知A的质量为1.32 kg,密度为1.1×10³ kg/m³,高为12 cm,B的底面积为60 cm².(g取10 N/kg)
(1)求A的重力.
(2)将B竖直放在水平桌面上,再将A竖直放在B的正上方,求A对B的压强.
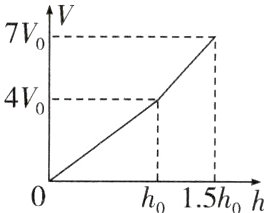
(3)将A竖直放入薄壁柱形容器中,向容器中缓慢加入液体直至加满,液体体积与液体深度的关系如图所示.用细线将A竖直向上提升2 cm时,细线的拉力为3.6 N,求液体的密度(圆柱体A始终处于竖直状态).
(1)求A的重力.
(2)将B竖直放在水平桌面上,再将A竖直放在B的正上方,求A对B的压强.
(3)将A竖直放入薄壁柱形容器中,向容器中缓慢加入液体直至加满,液体体积与液体深度的关系如图所示.用细线将A竖直向上提升2 cm时,细线的拉力为3.6 N,求液体的密度(圆柱体A始终处于竖直状态).

答案:
(1)$13.2\ N$
(2)$2.2\times10^{3}\ Pa$
(3)$0.8\times10^{3}\ kg/m^{3}$或$1.2\times10^{3}\ kg/m^{3}$ 解析:
(1)$A$的重力为:$G_{A} = m_{A}g = 1.32\ kg\times10\ N/kg = 13.2\ N$.
(2)由$\rho = \frac{m}{V}$可得$A$的体积为:$V_{A} = \frac{m_{A}}{\rho_{A}} = \frac{1.32\ kg}{1.1\times10^{3}\ kg/m^{3}} = 1.2\times10^{-3}\ m^{3}$,$A$的底面积为:$S_{A} = \frac{V_{A}}{h_{A}} = \frac{1.2\times10^{-3}\ m^{3}}{12\times10^{-2}\ m} = 0.01\ m^{2} = 100\ cm^{2}$,$S_{A}>S_{B}$,所以$A$与$B$的接触面积为$S = S_{B} = 60\ cm^{2}$,$A$对$B$的压强为:$p_{A} = \frac{G_{A}}{S} = \frac{13.2\ N}{60\times10^{-4}\ m^{2}} = 2.2\times10^{3}\ Pa$.
(3)结合图像信息可知:$\frac{4V_{0}}{h_{0}} = S_{容} - S_{A}$,$\frac{7V_{0} - 4V_{0}}{0.5h_{0}} = S_{容}$,$S_{容}:S_{A} = 3:1$,容器的底面积为:$S_{容} = 300\ cm^{2}$.
若$\rho_{A}>\rho_{液}$,对物体$A$受力分析如图:

物体$A$受到的竖直向下的重力与竖直向上的拉力和浮力相平衡,即$F_{浮} + F_{拉} = G_{A}$,所以物体$A$受到的浮力为:$F_{浮} = G_{A} - F_{拉} = 13.2\ N - 3.6\ N = 9.6\ N$,根据阿基米德原理$F_{浮} = \rho_{液}gV_{排}$和$V_{排} = V_{A}$知,$\rho_{液} = \frac{F_{浮}}{gV_{A}} = \frac{9.6\ N}{10\ N/kg\times1.2\times10^{-3}\ m^{3}} = 0.8\times10^{3}\ kg/m^{3}$;
若$\rho_{A}<\rho_{液}$,设液面下降的高度为$\Delta h$,如图:

物体$A$漂浮时,$F_{浮} = G_{A}$,细绳拉着时$\Delta F_{浮} = 3.6\ N$,物体受到的浮力变化量为:$\Delta F_{浮} = \rho_{液}g\Delta V_{排} = \rho_{液}gS_{A}(\Delta h + 0.02\ m)$,$S_{容}\times2\ cm = (S_{容} - S_{A})(2\ cm + \Delta h)$,解得$\Delta h = 1\ cm$;
$\Delta F_{浮} = \rho_{液}g\Delta V_{排} = \rho_{液}gS_{A}(\Delta h + 0.02\ m) = 3.6\ N$,解得液体的密度为:
$\rho_{液} = \frac{\Delta F_{浮}}{gS_{A}(\Delta h + 0.02\ m)} = \frac{3.6\ N}{10\ N/kg\times0.01\ m^{2}\times(0.01\ m + 0.02\ m)} = 1.2\times10^{3}\ kg/m^{3}$.
(1)$13.2\ N$
(2)$2.2\times10^{3}\ Pa$
(3)$0.8\times10^{3}\ kg/m^{3}$或$1.2\times10^{3}\ kg/m^{3}$ 解析:
(1)$A$的重力为:$G_{A} = m_{A}g = 1.32\ kg\times10\ N/kg = 13.2\ N$.
(2)由$\rho = \frac{m}{V}$可得$A$的体积为:$V_{A} = \frac{m_{A}}{\rho_{A}} = \frac{1.32\ kg}{1.1\times10^{3}\ kg/m^{3}} = 1.2\times10^{-3}\ m^{3}$,$A$的底面积为:$S_{A} = \frac{V_{A}}{h_{A}} = \frac{1.2\times10^{-3}\ m^{3}}{12\times10^{-2}\ m} = 0.01\ m^{2} = 100\ cm^{2}$,$S_{A}>S_{B}$,所以$A$与$B$的接触面积为$S = S_{B} = 60\ cm^{2}$,$A$对$B$的压强为:$p_{A} = \frac{G_{A}}{S} = \frac{13.2\ N}{60\times10^{-4}\ m^{2}} = 2.2\times10^{3}\ Pa$.
(3)结合图像信息可知:$\frac{4V_{0}}{h_{0}} = S_{容} - S_{A}$,$\frac{7V_{0} - 4V_{0}}{0.5h_{0}} = S_{容}$,$S_{容}:S_{A} = 3:1$,容器的底面积为:$S_{容} = 300\ cm^{2}$.
若$\rho_{A}>\rho_{液}$,对物体$A$受力分析如图:

物体$A$受到的竖直向下的重力与竖直向上的拉力和浮力相平衡,即$F_{浮} + F_{拉} = G_{A}$,所以物体$A$受到的浮力为:$F_{浮} = G_{A} - F_{拉} = 13.2\ N - 3.6\ N = 9.6\ N$,根据阿基米德原理$F_{浮} = \rho_{液}gV_{排}$和$V_{排} = V_{A}$知,$\rho_{液} = \frac{F_{浮}}{gV_{A}} = \frac{9.6\ N}{10\ N/kg\times1.2\times10^{-3}\ m^{3}} = 0.8\times10^{3}\ kg/m^{3}$;
若$\rho_{A}<\rho_{液}$,设液面下降的高度为$\Delta h$,如图:

物体$A$漂浮时,$F_{浮} = G_{A}$,细绳拉着时$\Delta F_{浮} = 3.6\ N$,物体受到的浮力变化量为:$\Delta F_{浮} = \rho_{液}g\Delta V_{排} = \rho_{液}gS_{A}(\Delta h + 0.02\ m)$,$S_{容}\times2\ cm = (S_{容} - S_{A})(2\ cm + \Delta h)$,解得$\Delta h = 1\ cm$;
$\Delta F_{浮} = \rho_{液}g\Delta V_{排} = \rho_{液}gS_{A}(\Delta h + 0.02\ m) = 3.6\ N$,解得液体的密度为:
$\rho_{液} = \frac{\Delta F_{浮}}{gS_{A}(\Delta h + 0.02\ m)} = \frac{3.6\ N}{10\ N/kg\times0.01\ m^{2}\times(0.01\ m + 0.02\ m)} = 1.2\times10^{3}\ kg/m^{3}$.
查看更多完整答案,请扫码查看


