《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

7. 设有一个经验回归方程为 $ \hat{y} = 2 - 1.5x $，则变量 $ x $ 增加一个单位时 (C)

A.$ y $ 平均增加 $ 1.5 $ 个单位
B.$ y $ 平均增加 $ 2 $ 个单位
C.$ y $ 平均减少 $ 1.5 $ 个单位
D.$ y $ 平均减少 $ 2 $ 个单位

答案： 7.C

8. 有人收集了春节期间平均气温 $ x $ 与某取暖商品的销售额 $ y $ 的有关数据如下表：

根据以上数据，用回归分析的方法，求得销售额 $ y $ 与平均气温 $ x $ 之间的经验回归方程 $ \hat{y} = \hat{b}x + \hat{a} $ 的系数 $ \hat{b} = -2.4 $，则预测平均气温为 $ -8 $℃时，该商品的销售额为 34.6 万元。

答案： 8.34.6[提示：由已知，得$\bar{x}=\frac{-2 - 3 - 5 - 6}{4}=-4$，$\bar{y}=\frac{20 + 23+27 + 30}{4}=25$，所以$\hat{a}=\bar{y}-\hat{b}\bar{x}=25 + 2.4×(-4)=15.4$，则经验回归方程为$\hat{y}=-2.4x + 15.4$，当$x = - 8$时，$\hat{y}=34.6$.]

1. 【题型一】对两个变量 $ y $ 和 $ x $ 进行回归分析，得到一组样本数据 $ (x_1,y_1),(x_2,y_2),·s,(x_n,y_n) $，则下列说法不正确的是 (C)

A.若变量 $ y $ 和 $ x $ 之间的样本相关系数为 $ r = -0.9462 $，则变量 $ y $ 和 $ x $ 之间具有较强的线性相关关系
B.残差平方和越小的模型，拟合的效果越好
C.用决定系数 $ R^2 $ 来刻画回归效果，$ R^2 $ 越小说明拟合效果越好
D.在残差图中，残差点分布水平带状区域的宽度越窄，则经验回归方程的预报精确度越高

答案： 1.C[提示：$|r|$越大，则变量$y$和$x$之间的线性相关性越强，故A正确；残差平方和越小的模型，拟合的效果越好，故B正确；用决定系数$R^{2}$来刻画回归效果，$R^{2}$越大说明拟合效果越好，故C错误；在残差图中，残差点分布水平带状区域的宽度越窄，则经验回归方程的预报精确度越高，故D正确.]

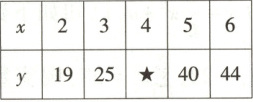
2. 【题型三】某工厂节能降耗技术改造后，在生产某产品过程中记录的产量 $ x $ (吨)与相应的生产能耗 $ y $ (吨)的几组对应数据如下表，现发现表中有个数据看不清，已知经验回归方程为 $ \hat{y} = 6.3x + 6.8 $，则看不清的数据 $ ★ $ 的值为 (A)


A.$ 32 $
B.$ 34 $
C.$ 36 $
D.$ 38 $

答案： 2.A[提示：设看不清的数据$\star$的值为$a$，则$\bar{x}=\frac{2 + 3+4 + 5+6}{5}=4$，$\bar{y}=\frac{19 + 25+a + 40+44}{5}=\frac{a + 128}{5}$，将样本点中心的坐标代入经验回归方程可得$6.3×4 + 6.8=\frac{a + 128}{5}$，解得$a = 32$.]

3. 【题型三】已知 $ x $ 与 $ y $ 之间的几组数据如下表：

假设根据上表数据所得经验回归方程为 $ \hat{y} = \hat{b}x + \hat{a} $，若某同学根据上表中的前两组数据 $ (1,0) $ 和 $ (2,2) $，求得的直线方程为 $ y = b'x + a' $，则以下结论正确的是 (D)

A.$ \hat{b} ＞ b' $，$ \hat{a} ＜ a' $
B.$ \hat{b} ＞ b' $，$ \hat{a} ＞ a' $
C.$ \hat{b} ＜ b' $，$ \hat{a} ＜ a' $
D.$ \hat{b} ＜ b' $，$ \hat{a} ＞ a' $

答案： 3.D[提示：由题意得$\bar{x}=\frac{7}{2}$，$\bar{y}=\frac{13}{6}$，$\sum_{i = 1}^{6}x_{i}^{2}=91$，$\sum_{i = 1}^{6}x_{i}y_{i}=58$，根据公式求得$\hat{b}=\frac{58 - 6×\frac{7}{2}×\frac{13}{6}}{91 - 6×(\frac{7}{2})^{2}}=\frac{5}{7}$，$\hat{a}=\bar{y}-\hat{b}\bar{x}=\frac{13}{6}-\frac{5}{7}×\frac{7}{2}=-\frac{1}{3}$，又$b'=2$，$a'=-2$，所以$\hat{b}＜b'$，$\hat{a}＞\hat{a}'.$]

4. 【题型二】(2025·黑龙江哈尔滨三中月考)为了研究变量 $ x $ 对变量 $ y $ 的影响，对变量 $ x $ 和变量 $ y $ 的观测数据 $ (x_i,y_i)(i = 1,2,·s,5) $ 进行研究，计算得到 $ \sum_{i = 1}^5 x_i y_i = 16.5 $，$ \sum_{i = 1}^5 x_i^2 = 55 $，若 $ y $ 与 $ x $ 满足一元线性回归模型 $ \begin{cases}Y = bx + e, \\ E(e) = 0, \\ D(e) = \sigma^2\end{cases}$，$ e $ 是 $ y $ 与 $ bx $ 之间的随机误差，则参数 $ b $ 的最小二乘估计为 ( )

A.$ 0.08 $
B.$ -0.08 $
C.$ 0.3 $
D.$ -0.3 $

答案： 4.C[提示：由题意知$y$与$x$满足的经验回归方程为$\hat{y}=\hat{b}x+\hat{e}$，残差平方和$\sum_{i = 1}^{n}e_{i}^{2}=\sum_{i = 1}^{n}(y_{i}-\hat{b}x_{i})^{2}=\sum_{i = 1}^{n}(y_{i}^{2}-2\hat{b}x_{i}y_{i}+\hat{b}^{2}x_{i}^{2})=\hat{b}^{2}\sum_{i = 1}^{n}x_{i}^{2}-2\hat{b}\sum_{i = 1}^{n}x_{i}y_{i}+\sum_{i = 1}^{n}y_{i}^{2}$，上式是关于$\hat{b}$的二次函数，因此要使残差平方和取得最小值，当且仅当$\hat{b}=\frac{\sum_{i = 1}^{n}x_{i}y_{i}}{\sum_{i = 1}^{n}x_{i}^{2}}=\frac{16.5}{55}=0.3$，故参数$\hat{b}$的最小二乘估计为$\hat{b}=0.3$.]

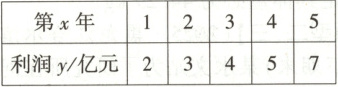
5. 【题型二、三】(2025·广西柳州模拟)[多选]某人工智能公司近 $ 5 $ 年的利润情况如下表所示：

已知变量 $ y $ 与 $ x $ 之间具有线性相关关系，设用最小二乘法建立的回归直线方程为 $ \hat{y} = 1.2x + \hat{a} $，则下列说法正确的是 (ACD)

A.$ \hat{a} = 0.6 $
B.变量 $ y $ 与 $ x $ 之间的线性相关系数 $ r ＜ 0 $
C.预测该人工智能公司第 $ 6 $ 年的利润约为 $ 7.8 $ 亿元
D.残差绝对值的最大值为 $ 0.4 $

答案： 5.ACD[提示：依题意得$\bar{x}=\frac{1}{5}(1 + 2+3 + 4+5)=3$，$\bar{y}=\frac{1}{5}(2 + 3+4 + 5+7)=\frac{21}{5}$，因为回归直线方程为$\hat{y}=1.2x+\hat{a}$必过样本中心点$(\bar{x},\bar{y})$，所以$\frac{21}{5}=1.2×3+\hat{a}$，解得$\hat{a}=0.6$，故A正确.回归直线方程为$\hat{y}=1.2x + 0.6$，所以$x$与$y$成正相关，即相关系数$r＞0$，故B错误.当$x = 6$时，$\hat{y}=1.2×6 + 0.6 = 7.8$，即该人工智能公司第$6$年的利润约为$7.8$亿元，故C正确.当$x = 1$时，$\hat{y}=1.2×1+0.6 = 1.8$，残差绝对值为$|1.8 - 2|=0.2$；当$x = 2$时，$\hat{y}=1.2×2+0.6 = 3$，残差绝对值为$|3 - 3|=0$；当$x = 3$时，$\hat{y}=1.2×3+0.6 = 4.2$，残差绝对值为$|4.2 - 4|=0.2$；当$x = 4$时，$\hat{y}=1.2×4+0.6 = 5.4$，残差绝对值为$|5.4 - 5|=0.4$；当$x = 5$时，$\hat{y}=1.2×5+0.6 = 6.6$，残差绝对值为$|6.6 - 7|=0.4$.所以残差绝对值的最大值为$0.4$，故D正确.]

6. 【题型二、三】(2025·广东佛山高三适应性考试)[多选]生活经验告诉我们，儿子的身高与父亲的身高不仅线性相关，而且还是正相关。有人调查了 $ 10 $ 名男大学生的身高 $ y $ (单位：$ cm $)及其父亲身高 $ x $ (单位：$ cm $)的数据 $ (x_i,y_i)(i = 1,2,·s,10) $，已知其中一组数据为 $ (182,185) $，且 $ \sum_{i = 1}^{10} x_i = 1750 $，求得经验回归方程为 $ \hat{y} = 0.65x + 63 $，并绘制了如图所示的残差图(残差 = 观测值 - 预测值)，则 (AC)


A.这 $ 10 $ 名男大学生的身高的平均值为 $ 176.75 $
B.由残差图可判定儿子身高与父亲身高的关系不符合上述回归模型
C.数据 $ (182,185) $ 对应的残差为 $ 3.7 $
D.去掉数据 $ (182,185) $ 后，重新求得的回归直线的决定系数 $ R^2 $ 变小
]

答案： 6.AC[提示：$(\bar{x},\bar{y})$满足经验回归方程，代入$x = 175$，计算可得$\hat{y}=176.75$，故A正确；从残差图中可以看到残差比较均匀地分布在以均值为$0$、横轴为对称轴的水平带状区域内，满足上述回归模型，故B错误；代入$x = 182$，得$\hat{y}=181.3$，因此残差为$185 - 181.3 = 3.7$，故C正确；由残差图可知$(182,185)$是一个极端数据，去掉后重新求得的回归直线拟合程度会变好，决定系数$R^{2}$变大，故D错误.]