2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
5. (2025·陕西咸阳高三联考)经过多年的发展,我国制造业的水平有了很大提高,出现了一批在国际上有影响的制造企业.我国的造船业、光伏产业、5G等已经在国际上处于领先地位,我国的精密制造也有了长足发展.已知某精密设备制造企业生产某种零件,根据长期检测结果得知,生产该零件的生产线的产品质量指标值服从正态分布$N(64,100)$,且质量指标值在$[54,84]$内的零件称为优等品.
(1)求该企业生产的零件为优等品的概率(结果精确到0.01);
(2)从该生产线生产的零件中随机抽取5件,随机变量$X$表示抽取的5件中优等品的件数,求$X$的分布列、数学期望和方差.
(参考数据:$P(\mu-\sigma\leq X\leq\mu+\sigma)\approx0.6827$,$P(\mu-2\sigma\leq X\leq\mu+2\sigma)\approx0.9545$,$P(\mu-3\sigma\leq X\leq\mu+3\sigma)\approx0.9973$)
(1)求该企业生产的零件为优等品的概率(结果精确到0.01);
(2)从该生产线生产的零件中随机抽取5件,随机变量$X$表示抽取的5件中优等品的件数,求$X$的分布列、数学期望和方差.
(参考数据:$P(\mu-\sigma\leq X\leq\mu+\sigma)\approx0.6827$,$P(\mu-2\sigma\leq X\leq\mu+2\sigma)\approx0.9545$,$P(\mu-3\sigma\leq X\leq\mu+3\sigma)\approx0.9973$)
答案:
5.解:
(1)因为产品质量指标值$X \sim N(64,10^{2})$,所以$\mu = 64$,$\sigma = 10$,所以优等品的概率$P(54 \leq X \leq 84)=P(54 \leq X \leq 64)+P(64 \leq X \leq 84)=P(\mu - \sigma \leq X \leq \mu)+P(\mu \leq X \leq \mu + 2\sigma)=\frac{1}{2} × 0.6827+\frac{1}{2} × 0.9545 \approx 0.82$,所以该企业生产零件为优等品的概率约为0.82.
(2)由
(1)知产品为优等品的概率为0.82,由题意知$X \sim B(5,0.82)$,随机变量X的取值为0,1,2,3,4,5,故$P(X = k)=C_{5}^{k}(0.82)^{k}(1 - 0.82)^{5 - k}(k = 0,1,2,3,4,5)$,即:
$X$ 0 1 2 3 4 5
$P$ $(0.18)^{5}$ $C_{5}^{1} × (0.82)^{1} × (0.18)^{4}$ $C_{5}^{2} × (0.82)^{2} × (0.18)^{3}$ $C_{5}^{3} × (0.82)^{3} × (0.18)^{2}$ $C_{5}^{4} × (0.82)^{4} × (0.18)^{1}$ $0.82^{5}$
所以$E(X)=5 × 0.82 = 4.1$,$D(X)=5 × 0.82 × 0.18 = 0.738$.
(1)因为产品质量指标值$X \sim N(64,10^{2})$,所以$\mu = 64$,$\sigma = 10$,所以优等品的概率$P(54 \leq X \leq 84)=P(54 \leq X \leq 64)+P(64 \leq X \leq 84)=P(\mu - \sigma \leq X \leq \mu)+P(\mu \leq X \leq \mu + 2\sigma)=\frac{1}{2} × 0.6827+\frac{1}{2} × 0.9545 \approx 0.82$,所以该企业生产零件为优等品的概率约为0.82.
(2)由
(1)知产品为优等品的概率为0.82,由题意知$X \sim B(5,0.82)$,随机变量X的取值为0,1,2,3,4,5,故$P(X = k)=C_{5}^{k}(0.82)^{k}(1 - 0.82)^{5 - k}(k = 0,1,2,3,4,5)$,即:
$X$ 0 1 2 3 4 5
$P$ $(0.18)^{5}$ $C_{5}^{1} × (0.82)^{1} × (0.18)^{4}$ $C_{5}^{2} × (0.82)^{2} × (0.18)^{3}$ $C_{5}^{3} × (0.82)^{3} × (0.18)^{2}$ $C_{5}^{4} × (0.82)^{4} × (0.18)^{1}$ $0.82^{5}$
所以$E(X)=5 × 0.82 = 4.1$,$D(X)=5 × 0.82 × 0.18 = 0.738$.
新考法2 跨学科融合
6. (2025·福建漳州三中高二下期中)[多选]如图,某电子实验猫线路图上有$A,B$两个即时红绿指示灯,当遇到红灯时,实验猫停止前行,恢复绿灯后,继续前行,$A,B$两个指示灯工作相互独立,且出现红灯的概率分别为$\frac{1}{2},p(0<p<1)$.同学甲从第一次实验到第五次实验中,实验猫在$A$处遇到红灯的次数为$X$,在$A,B$两处遇到红灯的次数之和为$Y$,则
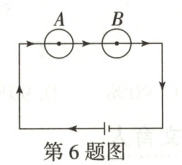
A.$P(X=3)=\frac{1}{32}$
B.$D(X)=\frac{5}{4}$
C.一次实验中,$A,B$两处至少遇到一次红灯的概率为$\frac{1}{2}+\frac{1}{2}p$
D.当$p=\frac{1}{3}$时,$E(Y)=\frac{25}{6}$
6. (2025·福建漳州三中高二下期中)[多选]如图,某电子实验猫线路图上有$A,B$两个即时红绿指示灯,当遇到红灯时,实验猫停止前行,恢复绿灯后,继续前行,$A,B$两个指示灯工作相互独立,且出现红灯的概率分别为$\frac{1}{2},p(0<p<1)$.同学甲从第一次实验到第五次实验中,实验猫在$A$处遇到红灯的次数为$X$,在$A,B$两处遇到红灯的次数之和为$Y$,则

A.$P(X=3)=\frac{1}{32}$
B.$D(X)=\frac{5}{4}$
C.一次实验中,$A,B$两处至少遇到一次红灯的概率为$\frac{1}{2}+\frac{1}{2}p$
D.当$p=\frac{1}{3}$时,$E(Y)=\frac{25}{6}$
答案:
6.BCD[提示:由题意可知$X \sim B(5,\frac{1}{2})$,所以$P(X = 3)=C_{5}^{3} × (\frac{1}{2})^{3} × (1 - \frac{1}{2})^{2}=\frac{10}{32}=\frac{5}{16}$,$D(X)=5 × \frac{1}{2} × (1 - \frac{1}{2})=\frac{5}{4}$,故A错误;一次实验中,A,B两处至少遇到一次红灯的概率为$1 - (1 - \frac{1}{2})(1 - \frac{1}{3})=\frac{1}{2} + \frac{1}{2} × \frac{1}{3}p$,故C正确;当$p = \frac{1}{3}$时,一次实验中没有遇到红灯的概率为$(1 - \frac{1}{2}) × (1 - \frac{1}{3})=\frac{1}{3}$,遇到一次红灯的概率为$\frac{1}{2} × (1 - \frac{1}{3})+(1 - \frac{1}{2}) × \frac{1}{3}=\frac{1}{3}$,遇到两次红灯的概率为$\frac{1}{2} × \frac{1}{3}=\frac{1}{6}$,所以一次实验中遇到红灯次数的数学期望为$0 × \frac{1}{3}+1 × \frac{1}{2}+2 × \frac{1}{6}=\frac{5}{6}$,所以$E(Y)=5 × \frac{5}{6}=\frac{25}{6}$,故D正确.]
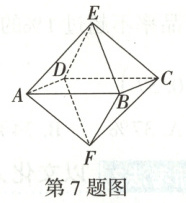
7. (2025·江苏南通一中高二下期末)六氟化硫在常压下是一种无色、无臭、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.已知六氟化硫分子构型呈正八面体(每个面都是正三角形),如图所示,任取正八面体的两条棱,在第一条棱取自四边形$ABCD$的一条边的条件下,再取第二条棱,则取出的两条棱所在的直线是异面直线的概率为
A.$\frac{2}{9}$
B.$\frac{4}{9}$
C.$\frac{2}{11}$
D.$\frac{4}{11}$

A.$\frac{2}{9}$
B.$\frac{4}{9}$
C.$\frac{2}{11}$
D.$\frac{4}{11}$
答案:
7.D[提示:假设取四边形ABCD中的AB,则与AB异面的直线为CE,DE,CF,DF,同理可得BC,CD,AD的异面直线,所以第一条棱取自四边形ABCD的一条边,第二次取的棱与第一次取的棱是异面直线的方法有$4 × 4$种,设事件M为“任取正八面体的两条棱”,第一条棱取自四边形ABCD的一条边”,事件N为“取的第二条棱与第一条棱成异面直线”,则任取正八面体的两条棱有$12 × 11$种方法,其中第一次取的棱是四边形ABCD的一条边有$4 × 11$种方法,所以$P(M)=\frac{4 × 11}{12 × 11}$,$P(MN)=\frac{4 × 4}{12 × 11}$,所以$P(N|M)=\frac{P(MN)}{P(M)}=\frac{4 × 4}{12 × 11} ÷ \frac{4 × 11}{12 × 11}=\frac{4}{11}$.]
新考法1 衔接新信息迁移问题
8. (2025·吉林延边二中高二下月考)贝叶斯在研究“逆向概率”的问题中得到了一个公式:$P(A|B)=\frac{P(B|A)· P(A)}{P(B|A)· P(A)+P(B|\overline{A})· P(\overline{A})}$.这个定理在实际生活中有着重要的应用价值.假设某种疾病在所有人群中的感染率是$0.1\%$,医院现有的技术对于该疾病检测的准确率为$99\%$,即已知患病情况下,$99\%$的可能性可以检查出阳性,正常人$99\%$的可能性检查为正常.如果从人群中随机抽一个人去检测,经计算检测结果为阳性的全概率为$0.01098$,请你用贝叶斯公式估计在医院给出的检测结果为阳性的条件下这个人得病的概率为
A.$0.1\%$
B.$8\%$
C.$9\%$
D.$99\%$
8. (2025·吉林延边二中高二下月考)贝叶斯在研究“逆向概率”的问题中得到了一个公式:$P(A|B)=\frac{P(B|A)· P(A)}{P(B|A)· P(A)+P(B|\overline{A})· P(\overline{A})}$.这个定理在实际生活中有着重要的应用价值.假设某种疾病在所有人群中的感染率是$0.1\%$,医院现有的技术对于该疾病检测的准确率为$99\%$,即已知患病情况下,$99\%$的可能性可以检查出阳性,正常人$99\%$的可能性检查为正常.如果从人群中随机抽一个人去检测,经计算检测结果为阳性的全概率为$0.01098$,请你用贝叶斯公式估计在医院给出的检测结果为阳性的条件下这个人得病的概率为
A.$0.1\%$
B.$8\%$
C.$9\%$
D.$99\%$
答案:
8.C[提示:记一个人得病为事件A,检测结果为阳性为事件B,则$P(A)=0.1\%$,$P(B|A)=99\%$,$P(B|A) · P(A)+P(B|A) · P(A)=0.01098$,所以$P(A|B)=\frac{P(B|A) · P(A)}{P(B|A) · P(A)+P(B|A) · P(A)}=\frac{99\% × 0.1\%}{0.01098} \approx 9\%$,所以在医院给出的检测结果为阳性的条件下这个人得病的概率为$9\%$.]
查看更多完整答案,请扫码查看


