《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

1. (教材改编题) 随机抛掷一颗均匀的正方体骰子,则骰子朝上的点数 $ X $ 的数学期望是 (B)

A.3
B.3.5
C.3.3
D.4

答案：
1.B[提示：抛掷正方体骰子朝上的点数X的分布列为：

所以$E(X)=\frac{1}{6} × (1+2+3+4+5+6)=3.5.$]

2. (教材改编题) 已知随机变量 $ X $ 的分布列如下表:

则 $ E(5X + 4) $ 等于 (D)

A.2.4
B.6.4
C.12
D.16

答案： 2.D[提示：由题意知$0.2+a+0.3=1$，解得$a=0.5$，所以$E(X)=1 × 0.2+2 × 0.5+4 × 0.3=2.4$，所以$E(5X+4)=5E(X)+4=5 × 2.4+4=16.$]

3. 一袋中装有 5 个球,编号分别为 1,2,3,4,5,在袋中同时取出 3 个,以 $ \xi $ 表示取出的三个球中的最小号码,则随机变量 $ \xi $ 的期望为$\frac{3}{2}$_ 。

答案： 3.$\frac{3}{2}$[提示：随机变量$\xi$的可能取值为$1,2,3,P(\xi=1)=\frac{C_{3}^{2}}{C_{5}^{3}}=\frac{3}{C_{5}^{3}},P(\xi=2)=\frac{C_{3}^{2}}{C_{5}^{3}}=\frac{3}{10},P(\xi=3)=\frac{C_{3}^{2}}{C_{5}^{3}}=\frac{1}{C_{5}^{3}}=\frac{1}{10},\therefore E(\xi)=1 × \frac{3}{5}+2 × \frac{3}{10}+3 × \frac{1}{10}=\frac{3}{2}.$]

4. 随机变量 $ X $ 的分布列如下表,其中 $ a,b,c $ 成等差数列,且 $ E(X)=\frac{1}{3} $。

(1) 求 $ a,b,c $ 的值;
(2) 求 $ E(3X + 1) $ 的值。

答案： 4.解：
(1)$\because a,b,c$成等差数列，$\therefore 2b=a+c$，又$a+b+c=1$，且$E(X)=-a+c=\frac{1}{3}$，联立以上三式解得$a=\frac{1}{6},b=\frac{1}{3},c=\frac{1}{2}$.
(2)由$E(X)=\frac{1}{3}$，得$E(3X+1)=3E(X)+1=2$.

5. 在 1,2,3,···,8 这 8 个自然数中任取 3 个数。
(1) 求这 3 个数中恰有 1 个偶数的概率;
(2) 设 $ X $ 为所取的 3 个数中奇数的个数,求随机变量 $ X $ 的分布列及均值。

答案：
5.解：
(1)这$3$个数中恰有$1$个偶数，则剩余$2$个数为奇数，设这$3$个数中恰有$1$个偶数为事件$A$，则$P(A)=\frac{C_{4}^{1}C_{4}^{2}}{C_{8}^{3}}=\frac{3}{7}$.
(2)$X$的可能取值为$0,1,2,3,P(X=0)=\frac{C_{4}^{0}C_{4}^{3}}{C_{8}^{3}}=\frac{1}{14},P(X=1)=\frac{C_{4}^{1}C_{4}^{2}}{C_{8}^{3}}=\frac{3}{7},P(X=2)=\frac{C_{4}^{2}C_{4}^{1}}{C_{8}^{3}}=\frac{3}{7},P(X=3)=\frac{C_{4}^{3}C_{4}^{0}}{C_{8}^{3}}=\frac{1}{14}$，
所以随机变量$X$的概率分布列为：
均值为$E(X)=0 × \frac{1}{14}+1 × \frac{3}{7}+2 × \frac{3}{7}+3 × \frac{1}{14}=\frac{3}{2}$.

6. (2025·重庆长寿中学高二下期中) 某次文化艺术展,以体现中华文化的外圆内方经典的古钱币造型作为该活动的举办标志,举办方计划在入口处设立一个如图所示的造型。现拟在图中五个不同的区域栽种花卉,要求相邻的两个区域的花卉品种不一样。

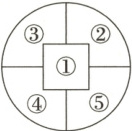
现有木绣球、玫瑰、广玉兰、锦带花、石竹 5 个不同的花卉品种。
(1) ①共有多少种不同的栽种方法?
②记“在区域③和区域⑤栽种不同的花卉”为事件 $ A $,“完成该标志花卉的栽种共用了 4 种不同的花卉”为事件 $ B $,求 $ P(A|B) $;
(2) 设完成该标志的栽种所用的花卉品种数为 $ \xi $,求 $ \xi $ 的分布列及期望。

答案：
6.解：
(1)①规定栽种顺序为：①$\rightarrow$③$\rightarrow$②$\rightarrow$④$\rightarrow$⑤，若②和④栽种同一种花卉，则栽种的方法数为$C_{5}^{1}C_{4}^{1}C_{3} × 3=180$；若②和④栽种不同花卉，则栽种的方法数为$C_{5}^{1}C_{4}^{1}C_{3} × 2 × 2=240$.
所以共有$180+240=420$种不同的栽种方法.
②由题意可知$P(AB)=\frac{C_{4}^{4}A_{4}^{4}}{420}=\frac{120}{420},P(B)=\frac{C_{4}^{1} × 2A_{4}^{4}}{420}=\frac{240}{420}$，所以$P(A|B)=\frac{P(AB)}{P(B)}=\frac{1}{2}$.
(2)由题意可知$\xi$可能的取值为$3,4,5$，则
$P(\xi=3)=\frac{C_{5}^{3}A_{3}^{3}}{420}=\frac{60}{420}=\frac{1}{7},P(\xi=4)=\frac{C_{5}^{1}A_{4}^{4} × 2}{420}=\frac{240}{420}=\frac{4}{7}$，
$P(\xi=5)=\frac{A_{5}^{5}}{420}=\frac{120}{420}=\frac{2}{7}$，所以$\xi$的分布列为：

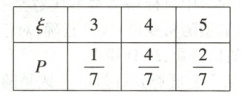
故期望为$E(\xi)=3 × \frac{1}{7}+4 × \frac{4}{7}+5 × \frac{2}{7}=\frac{29}{7}$.