《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

8. 【题型一、三】（2025·吉林长春二中月考）氮氧化物是一种常见的大气污染物，它是由氮和氧两种元素组成的化合物，有多种不同的形式。如图为我国2016年至2024年氮氧化物排放量（单位：万吨）的折线图，其中，年份代码1~9分别对应年份2016~2024。

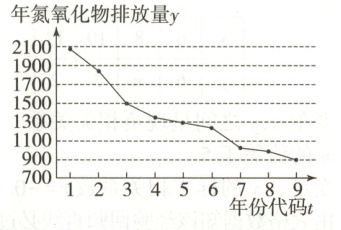
计算得$\sum_{i = 1}^{9}y_{i}=12200$，$\sqrt{\sum_{i = 1}^{9}(y_{i}-\overline{y})^{2}}=1125$，$\sum_{i = 1}^{9}t_{i}y_{i}=52640$。
(1) 是否可用线性回归模型拟合$y$与$t$的关系？请用折线图和相关系数加以说明。
(2) 是否可用题中数据拟合得到的线性回归模型预测2025年和2035年的氮氧化物排放量？请说明理由。
$\left(参考公式：相关系数r=\frac{\sum_{i = 1}^{n}(t_{i}-\overline{t})(y_{i}-\overline{y})}{\sqrt{\sum_{i = 1}^{n}(t_{i}-\overline{t})^{2}}\sqrt{\sum_{i = 1}^{n}(y_{i}-\overline{y})^{2}}},参考数据：\sqrt{15}\approx3.87\right)$

答案： 8. 解：
(1)从折线图看，各点近似落在一条直线附近，因而可以用线性回归模型拟合$y$与$t$的关系. 因为$\sum_{i = 1}^{9}(t_i - t)^2=\sum_{i = 1}^{9}(t_i - 5)^2 = 60$，所以该组数据的相关系数$r=\frac{\sum_{i = 1}^{9}(t_i - t)(y_i - \bar{y})}{\sqrt{\sum_{i = 1}^{9}(t_i - t)^2}·\sqrt{\sum_{i = 1}^{9}(y_i - \bar{y})^2}}=\frac{\sum_{i = 1}^{9}t_iy_i - 9t\bar{y}}{\sqrt{60}×\sqrt{\sum_{i = 1}^{9}(y_i - \bar{y})^2}}=\frac{52640 - 5×12200}{2\sqrt{15}×1125}\approx - 0.96$. 所以可以用线性回归模型拟合$y$与$t$的关系.
(2)可以用回归模型预测2025年的氮氧化物排放量，但不可以预测2035年的氮氧化物排放量，理由如下：①2025年与题中数据的年份较接近，因而可以认为短期内氮氧化物的排放量将延续
(1)中的线性趋势，故可以用
(1)中的回归模型进行预测；②2035年与题中数据的年份相距过远，而影响氮氧化物排放量的因素有很多，这些因素在短期内可能保持，但从长期角度看很有可能会变化，因而用
(1)中的回归模型预测是不准确的.

9. 【题型三】（2025·福建福州外国语学校高二下期中）某景区试卖一款纪念品，现统计了该款纪念品的定价x（单位：元）与销量y（单位：百件）的对应数据，如下表所示：

(1) 求该纪念品定价的平均值$\overline{x}$和销量的平均值$\overline{y}；$
(2) 计算x与y的相关系数；
(3) 由(2)的计算结果，判断能否用线性回归模型拟合y与x的关系，并说明理由。

答案： 9. 解：
(1)由题意可知$x=\frac{1}{5}(12 + 12.5 + 13 + 13.5 + 14)=13,y=\frac{1}{5}(14 + 13 + 11 + 9 + 8)=11$.
(2)计算得$\sum_{i = 1}^{5}(x_i - x)^2=2.5,\sum_{i = 1}^{5}(y_i - y)^2=26$，故$r=\frac{\sum_{i = 1}^{5}(x_i - x)(y_i - y)}{\sqrt{\sum_{i = 1}^{5}(x_i - x)^2}·\sqrt{\sum_{i = 1}^{5}(y_i - y)^2}}=-\frac{8}{\sqrt{65}}\approx - 0.992$.
(3)由
(2)可知$y$与$x$的相关系数的绝对值近似为$0.992$，非常接近$1$，说明$y$与$x$的线性相关性很强，从而可以用线性回归模型拟合$y$与$x$之间的关系.

为了比较甲、乙、丙、丁四组数据的线性相关性的强弱，某人分别计算了甲、乙、丙、丁四组数据的线性相关系数，其数值分别为$-0.95$，$0.87$，$0.58$，$0.92$，则这四组数据中线性相关性最强的是甲组数据。

答案： 甲[提示：因为线性相关系数的绝对值越大，线性相关性越强，所以甲组数据的线性相关性最强.]