《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

新考法1 聚焦热点情境，彰显时代特色
4. (2025·海南海口黄冈高二下月考)[多选]2025 海南国际康养产业博览会设有“气候治疗和气候康养产业合作”“食品营养健康”“森林康养产业发展”“医药大健康企业跨境出海”四大平行论坛。已知某医药公司的 4 位人员参与论坛，且每个人只能选一个论坛，则下列结论正确的有(AC)

A.每个论坛都有人员参与的情况共有 24 种
B.有论坛没人参与的情况共有 256 种
C.恰有 1 个论坛没人参与的情况共有 144 种
D.4 人只参与“食品营养健康”“森林康养产业发展”两个论坛的情况有 20 种

答案： 4. AC[提示：对于A，每个论坛都有人员参与的情况有$A_{4}^{4}=4×3×2×1 = 24$(种)，故A正确；对于B，4人参加四个论坛，每人只能去一个的总的情况有$4^{4}=256$(种)，所以有论坛没人参加的情况有$256 - 24 = 232$(种)，故B错误；对于C，恰有1个论坛没人参与的情况有$C_{4}^{1}C_{4}^{1}C_{3}^{2}A_{2}^{2}=144$(种)，故C正确；对于D，4人只参与“食品营养健康”“森林康养产业发展”两个论坛的情况有$C_{4}^{2}A_{2}^{2}+\frac{C_{4}^{2}C_{2}^{2}}{A_{2}^{2}}A_{2}^{2}=14$(种)，故D错误.]

5. (2025·吉林长春五中高二下期末)中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱。假设空间站要安排甲、乙、丙、丁、戊 5 名航天员开展实验，其中天和核心舱安排 1 人，问天实验舱与梦天实验舱各安排 2 人，且甲、乙两人被安排在同一个舱内，则共有方案(B)


A.3 种
B.6 种
C.30 种
D.60 种

答案： 5. B[提示：先从除甲、乙外的3名航天员中挑1人到天和核心舱有$C_{3}^{1}$种情况，然后剩下的2名航天员一组，甲、乙一组分配到剩下的两个舱有$A_{2}^{2}$种情况，所以共有$C_{3}^{1}A_{2}^{2}=6$(种).]

新考法2 跨学科融合
6. (2025·河南郑州一中高二下期末)已知生物体内存在酶 $ X $、酶 $ A $、酶 $ S $、酶 $ J $、酶 $ Y $，酶 $ X $ 可以与酶 $ A $、酶 $ S $、酶 $ J $、酶 $ Y $ 中的任意一种酶发生特异性结合反应。现有 3 个不同的酶 $ X $ 分子，每个酶 $ X $ 分子都随机选择一种酶进行结合，且相互独立，则不同的结合方式有(C)

A.72 种
B.68 种
C.64 种
D.58 种

答案： 6. C[提示：根据题意，酶$X$可以与酶$A$、酶$S$、酶$J$、酶$Y$中的任意一种酶发生特异性结合反应，即每一个酶$X$分子都有4种结合选择方式，那么3个不同的酶$X$分子的结合方式共有$4^{3}=64$(种).]

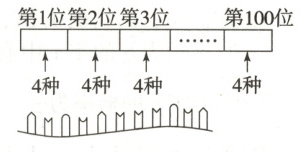
7. (2025·吉林长春东北师大附中周测)核糖核酸(RNA)分子是在生物细胞中发现的化学成分，一个 RNA 分子是一个有着数百个甚至数千个位置的长链，长链中每一个位置上都由一种称为碱基的化学成分所占据。总共有 4 种不同的碱基，分别用 $ A $，$ C $，$ G $，$ U $ 表示。在一个 RNA 分子中，各种碱基能够以任意次序出现，所以在任意一个位置上的碱基与其他位置上的碱基无关。假设有一类 RNA 分子由 100 个碱基组成(如图)，那么能有多少种不同的 RNA 分子？

答案： 7. 解：100个碱基组成的长链共有100个位置，从左到右依次在每一个位置中，从A，C，G，U中任选一个填入，每个位置有4种填充方法，根据分步乘法计数原理，长度为100的所有可能的不同RNA分子数目有$4^{100}$个.

新考法1 衔接新信息迁移问题
8. (2025·河南六校高三模拟)《孙子算经》是中国南北朝时期重要的数学著作，书中的“中国剩余定理”对同余除法进行了深入的研究。现给出一个同余问题：如果 $ a $ 和 $ b $ 被 $ m $ 除得的余数相同，那么称 $ a $ 和 $ b $ 对模 $ m $ 同余，记为 $ a \equiv b(\bmod m) $。若 $ a $ 为 $ (4 + x)^{2024} $ 的二项展开式中含 $ x $ 项的系数，且 $ a \equiv b(\bmod 5) $，则 $ b $ 的值可以是(D)

A.203
B.204
C.205
D.206

答案： 8. D[提示：$(4 + x)^{2024}$的二项展开式中含$x$项的系数为$C_{2024}^{1}4^{2023}=2024×4^{2023}$，由二项式定理可得$2024×(5 - 1)^{2023}=2024×\sum_{i = 0}^{2022}C_{2023}^{i}5^{2023 - i}(-1)^{i}-2025 + 1$，而$2024×\sum_{i = 0}^{2022}C_{2023}^{i}5^{2023 - i}(-1)^{i}-2025$能被5整除，所以$2024×(5 - 1)^{2023}$除以5的余数为1，而$b,a$除以5的余数相同，所以$b$除以5的余数为1，而$203 = 5×40 + 3$，$205 = 5×41$，$204 = 5×40 + 4$，$206 = 5×41 + 1$，故D正确.]

9. (2025·河北沧州一中高二下月考)[多选]在光纤通信中，用光信号的不同强度或状态来代表二进制中的 1 和 0，因此常用 0 和 1 组成的有序数组 $ u = (a_{1}, a_{2}, a_{3}, ·s, a_{i}, ·s, a_{n})(i, n \in N^{*}, 1 \leq i \leq n, a_{i} = 0 $ 或 $ 1) $ 的形式表示信息，$ u $ 被称为一个长为 $ n $ 的字，设 $ u = (a_{1}, a_{2}, a_{3}, ·s, a_{i}, ·s, a_{n}) $，$ v = (b_{1}, b_{2}, b_{3}, ·s, b_{i}, ·s, b_{n}) $ 分别为两个长为 $ n $ 的字，令 $ d(u, v) $ 表示使 $ a_{i} \neq b_{i} $ 的 $ i(1 \leq i \leq n) $ 的个数，例如 $ u = (0, 1, 0) $，$ v = (1, 1, 0) $，$ w = (1, 1, 1) $，则 $ d(u, v) = 1 $，$ d(u, w) = 2 $。下列命题正确的是(AC)

A.若 $ u = (0, 1, 0, 1) $，$ v = (1, 1, 1, 0) $，则 $ d(u, v) = 3 $
B.若 $ u = (0, 1, 0, 0, 1) $，则满足 $ d(u, v) = 2 $，字长为 5 的字 $ v $ 的个数为 5
C.若 $ u = (1, 0, 1, 0, 0, 1) $，则满足 $ d(u, v) = 3 $，字长为 6 的字 $ v $ 中有且仅有 3 个 1 相邻的字 $ v $ 的概率为 $ \frac{1}{5} $
D.若 $ w = (\underbrace{1, 1, 1, ·s, 1, 1, 1}_{n 个 1}) $，$ u = (a_{1}, a_{2}, a_{3}, ·s, a_{i}, ·s, a_{n}) $，$ v = (b_{1}, b_{2}, b_{3}, ·s, b_{i}, ·s, b_{n}) $，则 $ d(u, v) \geq d(u, w) + d(v, w) $

答案： 9. AC[提示：对于A，$u=(0,1,0,1)$，$v=(1,1,1,0)$，则$d(u,v)=3$，故A正确；对于B，若$u=(0,1,0,0,1)$，则满足$d(u,v)=2$，字长为5的字$v$的个数为$C_{5}^{2}=10$，故B不正确；对于C，若$u=(1,0,1,0,0,1)$，则满足$d(u,v)=3$，字长为6的字$v$的个数为$C_{6}^{3}=20$，其中有且仅有3个1相邻的字$v$分别为$(1,1,1,0,1,0)$，$(0,1,1,1,0,1)$，$(1,0,1,1,1,0)$，$(1,0,0,1,1,1)$，所以所求概率为$\frac{4}{20}=\frac{1}{5}$，故C正确；对于D，可举反例，不妨令$n = 6$，则$w=(1,1,1,1,1,1)$，$u=(0,0,1,1,1,1)$，$v=(0,1,0,1,0,0)$，所以$d(u,w)=2$，$d(v,w)=4$，$d(u,v)=4$，此时$d(u,v)\lt d(u,w)+d(v,w)$，故D不正确.]