2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
10. 某地区$3000$名高三学生在某次模拟考试中的总分$X$服从正态分布$N ( 550, 50 ^ { 2 } )$。
(1) 求$P ( 500 \leqslant X \leqslant 650 )$;
(2) 试估计该地区$3000$名高三学生中总分$X$落在区间$( 600, 700 ]$的人数.
(参考数据:$P ( \mu - \sigma \leqslant X \leqslant \mu + \sigma ) \approx 0. 6827$,$P ( \mu - 2 \sigma \leqslant X \leqslant \mu + 2 \sigma ) \approx 0. 9545$,$P ( \mu - 3 \sigma \leqslant X \leqslant \mu + 3 \sigma ) \approx 0. 9973$)
(1) 求$P ( 500 \leqslant X \leqslant 650 )$;
(2) 试估计该地区$3000$名高三学生中总分$X$落在区间$( 600, 700 ]$的人数.
(参考数据:$P ( \mu - \sigma \leqslant X \leqslant \mu + \sigma ) \approx 0. 6827$,$P ( \mu - 2 \sigma \leqslant X \leqslant \mu + 2 \sigma ) \approx 0. 9545$,$P ( \mu - 3 \sigma \leqslant X \leqslant \mu + 3 \sigma ) \approx 0. 9973$)
答案:
10.解:
(1)由题知$\mu = 550$,$\sigma = 50$,则$500 = \mu - \sigma$,$650 = \mu + 2\sigma$,所以$P(500\leq X\leq650)=P(\mu - \sigma\leq X\leq\mu + 2\sigma)=\frac{1}{2}[P(\mu - \sigma\leq X\leq\mu + \sigma)+P(\mu - 2\sigma\leq X\leq\mu + 2\sigma)]\approx0.8186$。
(2)因为$600 = \mu + \sigma$,$700 = \mu + 3\sigma$,所以$P(600<X\leq700)=P(\mu + \sigma<X\leq\mu + 3\sigma)=\frac{1}{2}[P(\mu - 3\sigma\leq X\leq\mu + 3\sigma)-P(\mu - \sigma\leq X\leq\mu + \sigma)]\approx0.1573$,因为$3000×0.1573 = 471.9\approx472$,所以该地区3000名高三学生中,总分$X$落在区间$(600,700]$的人数约为472。
(1)由题知$\mu = 550$,$\sigma = 50$,则$500 = \mu - \sigma$,$650 = \mu + 2\sigma$,所以$P(500\leq X\leq650)=P(\mu - \sigma\leq X\leq\mu + 2\sigma)=\frac{1}{2}[P(\mu - \sigma\leq X\leq\mu + \sigma)+P(\mu - 2\sigma\leq X\leq\mu + 2\sigma)]\approx0.8186$。
(2)因为$600 = \mu + \sigma$,$700 = \mu + 3\sigma$,所以$P(600<X\leq700)=P(\mu + \sigma<X\leq\mu + 3\sigma)=\frac{1}{2}[P(\mu - 3\sigma\leq X\leq\mu + 3\sigma)-P(\mu - \sigma\leq X\leq\mu + \sigma)]\approx0.1573$,因为$3000×0.1573 = 471.9\approx472$,所以该地区3000名高三学生中,总分$X$落在区间$(600,700]$的人数约为472。
1. 【题型二】(2025·黑龙江哈尔滨三中高三模拟) 已知随机变量$X$服从标准正态分布$N ( 0, 1 )$,且$P ( X \geqslant a ) = 0. 3$,则$P ( - a \leqslant X < 0 )$等于 (
A.$0. 1$
B.$0. 2$
C.$0. 3$
D.$0. 6$
B
)A.$0. 1$
B.$0. 2$
C.$0. 3$
D.$0. 6$
答案:
1.B[提示:由题意,随机变量$X$服从标准正态分布$N(0,1)$,所以$\mu = 0$,因为$P(X\geq a)=0.3$,所以$P(X\leq - a)=0.3$,所以$P(-a\leq X\leq a)=1 - P(X\geq a)-P(X\leq - a)=1 - 0.3 - 0.3 = 0.4$,所以$P(-a\leq X<0)=\frac{1}{2}P(-a\leq X\leq a)=0.2$。]
2. 【题型一】(2025·黑龙江哈尔滨三中高二下月考) 随机变量$X$,$Y$满足$X \sim B \left( 4, \frac { 1 } { 2 } \right)$,$Y \sim N ( 2, 4 )$,则下列选项正确的是 (
A.$E ( X ) = E ( Y )$
B.$D ( X ) = D ( Y )$
C.$P ( X = 2 ) = \frac { 1 } { 2 }$
D.$P ( Y > 2 ) = P ( Y < 0 )$
A
)A.$E ( X ) = E ( Y )$
B.$D ( X ) = D ( Y )$
C.$P ( X = 2 ) = \frac { 1 } { 2 }$
D.$P ( Y > 2 ) = P ( Y < 0 )$
答案:
2.A[提示:由二项分布和正态分布可知$E(X)=4×\frac{1}{2}=2$,$D(X)=4×\frac{1}{2}×(1 - \frac{1}{2}) = 1$,$E(Y)=2$,$D(Y)=4$,故A正确,B错误;对于C,$P(X = 2)=C_{4}^{2}×(\frac{1}{2})^2×(1 - \frac{1}{2})^2=\frac{3}{8}$,故C错误;对于D,根据正态分布可知$\mu = 2$,所以$P(Y>2)=P(Y>\mu)=\frac{1}{2}$,$P(Y<0)<P(Y<2)=P(Y<\mu)=\frac{1}{2}$,所以$P(Y>2)>P(Y<0)$,故D错误。]
3. 【题型一】(2025·吉林通化五中高二下月考) 已知连续型随机变量$\xi$服从正态分布$N \left( \frac { 1 } { 2 }, \frac { 1 } { 4 } \right)$,记函数$f ( x ) = P ( \xi \leqslant x )$,则$f ( x )$的图象 (
A.关于直线$x = \frac { 1 } { 2 }$对称
B.关于直线$x = \frac { 1 } { 4 }$对称
C.关于点$\left( \frac { 1 } { 2 }, \frac { 1 } { 2 } \right)$成中心对称
D.关于点$\left( \frac { 1 } { 4 }, \frac { 1 } { 4 } \right)$成中心对称
C
)A.关于直线$x = \frac { 1 } { 2 }$对称
B.关于直线$x = \frac { 1 } { 4 }$对称
C.关于点$\left( \frac { 1 } { 2 }, \frac { 1 } { 2 } \right)$成中心对称
D.关于点$\left( \frac { 1 } { 4 }, \frac { 1 } { 4 } \right)$成中心对称
答案:
3.C[提示:由连续型随机变量$\xi$服从正态分布$N(\frac{1}{2},\frac{1}{4})$,可得$\mu=\frac{1}{2}$,$\sigma^2=\frac{1}{4}$,所以$\mu=\frac{1}{2}$,$\sigma=\frac{1}{2}$,所以正态密度曲线关于直线$x=\frac{1}{2}$对称,即$P(\xi\leq x)=P(\xi\geq1 - x)$,由$f(x)=P(\xi\leq x)$,可得$f(x)=P(\xi\leq x)$在$x\leq\frac{1}{2}$时增加较快,在$x>\frac{1}{2}$时增加越来越慢,所以$f(x)$无对称轴,故A,B错误;$f(x)+f(1 - x)=P(\xi\leq x)+P(\xi\leq1 - x)=P(\xi\geq1 - x)+P(\xi\leq1 - x)=1$,所以$f(x)$的图象关于点$(\frac{1}{2},\frac{1}{2})$成中心对称,故C正确,D错误。]
4. 【题型一】已知随机变量$X \sim B ( 6, p )$,$Y \sim N ( \mu, \sigma ^ { 2 } )$,且$P ( Y \geqslant 2 ) = \frac { 1 } { 2 }$,$E ( X ) = E ( Y )$,则$p$等于 (
A.$\frac { 1 } { 2 }$
B.$\frac { 1 } { 3 }$
C.$\frac { 1 } { 4 }$
D.$\frac { 1 } { 6 }$
B
)A.$\frac { 1 } { 2 }$
B.$\frac { 1 } { 3 }$
C.$\frac { 1 } { 4 }$
D.$\frac { 1 } { 6 }$
答案:
4.B[提示:因为随机变量$X\sim B(6,p)$,所以$E(X)=6p$,因为$Y\sim N(\mu,\sigma^2)$,$P(Y\geq2)=\frac{1}{2}$,所以$\mu = 2$,即$E(Y)=2$,又$E(X)=E(Y)$,所以$6p = 2$,即$p=\frac{1}{3}$。]
5. 【题型一】设$X \sim N ( \mu _ { 1 }, \sigma _ { 1 } ^ { 2 } )$,$Y \sim N ( \mu _ { 2 }, \sigma _ { 2 } ^ { 2 } )$,这两个正态密度曲线如图所示,下列结论中正确的是 (
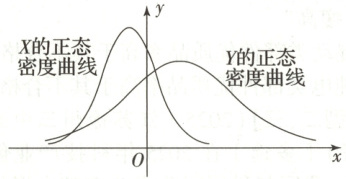
A.$\mu _ { 1 } > \mu _ { 2 }$
B.$\sigma _ { 1 } > \sigma _ { 2 }$
C.$P ( Y \geqslant \mu _ { 2 } ) \geqslant P ( Y \geqslant \mu _ { 1 } )$
D.$P ( X \leqslant \mu _ { 2 } ) \geqslant P ( X \leqslant \mu _ { 1 } )$
D
)
A.$\mu _ { 1 } > \mu _ { 2 }$
B.$\sigma _ { 1 } > \sigma _ { 2 }$
C.$P ( Y \geqslant \mu _ { 2 } ) \geqslant P ( Y \geqslant \mu _ { 1 } )$
D.$P ( X \leqslant \mu _ { 2 } ) \geqslant P ( X \leqslant \mu _ { 1 } )$
答案:
5.D[提示:因为$X\sim N(\mu_1,\sigma_1^2)$,$Y\sim N(\mu_2,\sigma_2^2)$,两曲线分别关于直线$x = \mu_1$,$x = \mu_2$对称,所以由图可知$\mu_1<\mu_2$,所以A错误;因为$X$的正态曲线“瘦高”,$Y$的正态曲线“矮胖”,所以$\sigma_1<\sigma_2$,所以B错误;所以$P(Y\geq\mu_2)\leq P(Y\geq\mu_1)$,$P(X\leq\mu_1)\geq P(X\leq\mu_1)$,所以C错误,D正确。]
6. 【题型一】设随机变量$\xi$服从正态分布$N ( 2, 9 )$,若$P ( \xi < 2 m + 1 ) = P ( \xi > m - 1 )$,则实数$m$的值是 (
A.$\frac { 2 } { 3 }$
B.$\frac { 4 } { 3 }$
C.$\frac { 5 } { 3 }$
D.$2$
B
)A.$\frac { 2 } { 3 }$
B.$\frac { 4 } { 3 }$
C.$\frac { 5 } { 3 }$
D.$2$
答案:
6.B[提示:因为随机变量$\xi$服从正态分布$N(2,9)$,$P(\xi<2m + 1)=P(\xi>m - 1)$,根据正态分布的特征,可得$\frac{2m + 1 + m - 1}{2}=2$,解得$m=\frac{4}{3}$。]
7. 【题型三】(2025·辽宁葫芦岛一中高二下月考) [多选] 现对跑完某次$5$公里马拉松的$1000$名参与者的完成时间$t$ (单位:分钟)进行统计,得到这$1000$名参与者的完成时间$t$近似服从正态分布$N ( 20, 1. 44 )$,则 (
(参考数据:若$X \sim N ( \mu, \sigma ^ { 2 } )$,则$P ( \mu - \sigma < X \leqslant \mu + \sigma ) \approx 0. 683$,$P ( \mu - 2 \sigma < X \leqslant \mu + 2 \sigma ) \approx 0. 954$,$P ( \mu - 3 \sigma < X \leqslant \mu + 3 \sigma ) \approx 0. 997$)
A.这跑完全程的$1000$名参与者中大约有$683$人的完成时间在$( 18. 8, 21. 2 ]$内
B.这跑完全程的$1000$名参与者中大约有$477$人的完成时间在$( 20, 22. 4 ]$内
C.这跑完全程的$1000$名参与者中大约有$954$人的完成时间在$( 17. 6, 23. 6 ]$内
D.这跑完全程的$1000$名参与者中完成时间在$( 17. 6, 21. 2 ]$内与在$( 18. 8, 22. 4 ]$内的人数大致相等
ABD
)(参考数据:若$X \sim N ( \mu, \sigma ^ { 2 } )$,则$P ( \mu - \sigma < X \leqslant \mu + \sigma ) \approx 0. 683$,$P ( \mu - 2 \sigma < X \leqslant \mu + 2 \sigma ) \approx 0. 954$,$P ( \mu - 3 \sigma < X \leqslant \mu + 3 \sigma ) \approx 0. 997$)
A.这跑完全程的$1000$名参与者中大约有$683$人的完成时间在$( 18. 8, 21. 2 ]$内
B.这跑完全程的$1000$名参与者中大约有$477$人的完成时间在$( 20, 22. 4 ]$内
C.这跑完全程的$1000$名参与者中大约有$954$人的完成时间在$( 17. 6, 23. 6 ]$内
D.这跑完全程的$1000$名参与者中完成时间在$( 17. 6, 21. 2 ]$内与在$( 18. 8, 22. 4 ]$内的人数大致相等
答案:
7.ABD[提示:根据时间$t$近似服从正态分布$N(20,1.44)$,可得$P(18.8<t\leq21.2)\approx0.683$,$P(17.6<t\leq22.4)\approx0.954$,$P(16.4<t<23.6)\approx0.997$,所以跑完全程的1000名参与者中完成时间在$(18.8,21.2]$内的大约有:$1000×0.683 = 683$(人),故A正确;由$P(17.6<t\leq22.4)\approx0.954$可知$P(20<t\leq22.4)=\frac{0.954}{2}=0.477$,所以跑完全程的1000名参与者中完成时间在$(20,22.4]$内的大约有:$1000×0.477 = 477$(人),故B正确;由$P(17.6<t\leq22.4)\approx0.954$,$P(16.4<t<23.6)\approx0.997$,可知$P(17.6<t\leq23.6)\approx\frac{0.954}{2}+\frac{0.997}{2}=0.9755$,所以跑完全程的1000名参与者中完成时间在$(17.6,23.6]$内的大约有$1000×0.9755\approx976$(人),故C错误;由正态分布的对称性可知$P(17.6<t\leq21.2)=P(18.8<t\leq22.4)$,所以跑完全程的1000名参与者中完成时间在$(17.6,21.2]$内与在$(18.8,22.4]$内的人数大致相等,故D正确。]
查看更多完整答案,请扫码查看


