2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. (2025·吉林长春二中月考) [多选] 已知三个正态分布密度函数$\varphi _ { i } ( x ) = \frac { 1 } { \sqrt { 2 \pi } \sigma _ { i } } \mathrm { e } ^ { - \frac { ( x - \mu _ { i } ) ^ { 2 } } { 2 \sigma _ { i } ^ { 2 } } } ( i = 1, 2, 3 )$的图象如图所示,下列关于$\mu _ { 1 }, \mu _ { 2 }, \mu _ { 3 }, \sigma _ { 1 }, \sigma _ { 2 }, \sigma _ { 3 }$的大小关系正确的是 (
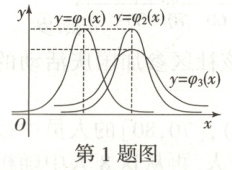
A.$\mu _ { 1 } < \mu _ { 2 } = \mu _ { 3 }$
B.$\sigma _ { 1 } = \sigma _ { 2 } < \sigma _ { 3 }$
C.$\mu _ { 1 } > \mu _ { 2 } = \mu _ { 3 }$
D.$\sigma _ { 1 } = \sigma _ { 2 } > \sigma _ { 3 }$
AB
)
A.$\mu _ { 1 } < \mu _ { 2 } = \mu _ { 3 }$
B.$\sigma _ { 1 } = \sigma _ { 2 } < \sigma _ { 3 }$
C.$\mu _ { 1 } > \mu _ { 2 } = \mu _ { 3 }$
D.$\sigma _ { 1 } = \sigma _ { 2 } > \sigma _ { 3 }$
答案:
1.AB[提示:正态分布曲线关于直线$x = \mu$对称,且$\mu$越大图象的对称轴越靠近右边,所以第一个曲线的均值比第二和第三的均值小,且第二、三个的均值相等,所以$\mu_1 < \mu_2 = \mu_3$。$\sigma$越小,曲线越瘦高,所以第二个图象的$\sigma$要比第三个的$\sigma$要小,故$\sigma_1 = \sigma_2 < \sigma_3$。]
2. 三个正态分布$X \sim N ( 0, 0. 64 )$,$Y \sim N ( 0, 1 )$,$Z \sim N ( 0, 4 )$对应的正态密度曲线如图所示,则三个随机变量$X$,$Y$,$Z$对应曲线的序号依次为 (
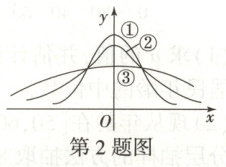
A.①②③
B.③②①
C.②③①
D.①③②
A
)
A.①②③
B.③②①
C.②③①
D.①③②
答案:
2.A[提示:由题意,得$\sigma(X)=0.8$,$\sigma(Y)=1$,$\sigma(Z)=2$,因为当$\sigma$较小时,正态曲线“瘦高”,且$\sigma(X)<\sigma(Y)<\sigma(Z)$,所以三个随机变量$X$,$Y$,$Z$对应曲线的序号依次为①②③。]
3. (教材改编题) 某市教育局为了解高三学生的学习情况,组织了一次摸底考试,共有$40000$名考生参加这次考试,数学成绩$X$近似服从正态分布,其正态密度函数为$f ( x ) = \frac { 1 } { \sigma \sqrt { 2 \pi } } \mathrm { e } ^ { - \frac { ( x - 90 ) ^ { 2 } } { 2 \sigma ^ { 2 } } }, x \in \mathbf { R }$且$P ( 70 \leqslant X \leqslant 110 ) = 0. 8$,则该市这次考试数学成绩超过$110$分的考生人数约为 (
A.$2000$
B.$3000$
C.$4000$
D.$8000$
C
)A.$2000$
B.$3000$
C.$4000$
D.$8000$
答案:
3.C[提示:由题知均值$\mu = 90$,由正态曲线的对称性可知$P(X>110)=0.5 - \frac{1}{2}P(70\leq X\leq110)=0.5 - 0.4 = 0.1$,所以该市这次考试数学成绩超过110分的考生人数约为$0.1×40000 = 4000$。]
4. 甲、乙两名高中同学历次数学测试成绩(百分制)分别服从正态分布$N ( \mu _ { 1 }, \sigma _ { 1 } ^ { 2 } )$,$N ( \mu _ { 2 }, \sigma _ { 2 } ^ { 2 } )$,对应的正态密度曲线如图所示,则下列说法中不正确的是 (
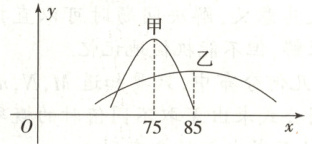
(参考数据:若随机变量$X$服从正态分布$N ( \mu, \sigma ^ { 2 } )$,则$P ( \mu - \sigma \leqslant X \leqslant \mu + \sigma ) \approx 0. 6827$)
A.乙同学的平均成绩优于甲同学的平均成绩
B.甲同学的平均成绩优于乙同学的平均成绩
C.甲同学的成绩比乙同学成绩更集中于平均值附近
D.若$\sigma _ { 1 } = 5$,则甲同学成绩高于$80$分的概率约为$0. 1587$
B
)
(参考数据:若随机变量$X$服从正态分布$N ( \mu, \sigma ^ { 2 } )$,则$P ( \mu - \sigma \leqslant X \leqslant \mu + \sigma ) \approx 0. 6827$)
A.乙同学的平均成绩优于甲同学的平均成绩
B.甲同学的平均成绩优于乙同学的平均成绩
C.甲同学的成绩比乙同学成绩更集中于平均值附近
D.若$\sigma _ { 1 } = 5$,则甲同学成绩高于$80$分的概率约为$0. 1587$
答案:
4.B[提示:由图象可知,甲的图象关于直线$x = 75$对称,乙的图象关于直线$x = 85$对称,所以甲同学的平均成绩为75分,乙同学的平均成绩为85分,故选项A的说法正确,B的说法错误;因为甲的图象比乙的图象更“瘦高”,所以甲的成绩比乙的成绩更集中于平均值左右,故选项C的说法正确;若$\sigma_1 = 5$,则甲同学成绩高于80分的概率约为$\frac{1 - 0.6827}{2}\approx0.1587$,故选项D的说法正确。]
5. 若随机变量$X$的正态密度函数为$f _ { \mu, \sigma } ( x ) = \frac { 1 } { \sqrt { 2 \pi } \sigma } \mathrm { e } ^ { - \frac { ( x - \mu ) ^ { 2 } } { 2 \sigma ^ { 2 } } }, x \in ( - \infty, + \infty )$ (其中$\mu \in \mathbf { R }$,$\sigma > 0$为参数),其图象如图所示,则$X$的均值为
 ]
]
20
,方差为2
。 ]
]
答案:
5.20 2[提示:由图可知该正态曲线关于直线$x = 20$对称,最大值是$\frac{1}{2\sqrt{\pi}}$,所以$\mu = 20$,由$\frac{1}{2\sqrt{\pi}\sigma}=\frac{1}{2\sqrt{\pi}}$,解得$\sigma=\sqrt{2}$,所以随机变量$X$的均值是$\mu = 20$,方差是$\sigma^2 = (\sqrt{2})^2 = 2$。]
6. 已知随机变量$X$服从正态分布$N ( 3, \sigma ^ { 2 } )$,且$P ( X < 5 ) = 0. 8$,则$P ( X < 3 ) = $
0.5
,$P ( 1 < X < 3 ) = $0.3
。
答案:
6.0.5 0.3[提示:由正态曲线的对称性可知$P(X<3)=P(X>3)=0.5$,$P(X>1)=P(X<5)=0.8$,所以$P(X\leq1)=1 - P(X>1)=0.2$,所以$P(1<X<3)=P(X<3)-P(X\leq1)=0.5 - 0.2 = 0.3$。]
7. 若随机变量$\xi \sim N ( 2, \sigma ^ { 2 } ) ( \sigma > 0 )$,$P ( \xi \leqslant 3 ) = 0. 9$,则$P ( 1 \leqslant \xi < 2 ) = $
0.4
。
答案:
7.0.4[提示:由正态分布曲线的对称性可知$P(1\leq\xi<2)=\frac{1 - 2[1 - P(\xi\leq3)]}{2}=0.4$。]
8. (教材改编题) 某市$20000$名学生参加一次数学测试(满分$150$分),学生的测试成绩$X$近似服从正态分布$N ( 100, 10 ^ { 2 } )$,则测试成绩在$[ 90, 100 ]$内的学生人数约为
6827
人. (参考数据:若$X \sim N ( \mu, \sigma ^ { 2 } )$,则$P ( \mu - \sigma \leqslant X \leqslant \mu + \sigma ) \approx 0. 6827$,$P ( \mu - 2 \sigma \leqslant X \leqslant \mu + 2 \sigma ) \approx 0. 9545$)
答案:
8.6827[提示:因为$P(90\leq X\leq100)=P(\mu - \sigma\leq X\leq\mu)=\frac{1}{2}P(\mu - \sigma\leq X\leq\mu + \sigma)\approx\frac{1}{2}×0.6827 = 0.34135$,所以测试成绩在$[90,100]$内的学生人数约为$20000×0.34135 = 6827$。]
9. 为了解高三复习备考情况,某校组织了一次阶段考试. 若高三全体考生的数学成绩$X$近似服从正态分布$N ( 100, 17. 5 ^ { 2 } )$,已知成绩在$117. 5$分以上(含$117. 5$分)的学生有$80$人,则此次参加考试的学生成绩不超过$82. 5$分的概率为
0.16
;如果成绩大于$135$分的为特别优秀,那么本次考试数学成绩特别优秀的大约有10
人. (参考数据:若$X \sim N ( \mu, \sigma ^ { 2 } )$,则$P ( \mu - \sigma < X < \mu + \sigma ) \approx 0. 68$,$P ( \mu - 2 \sigma < X < \mu + 2 \sigma ) \approx 0. 96$)
答案:
9.0.16 10[提示:由题知$P(X\leq82.5)=P(X\leq\mu - \sigma)=\frac{1 - P(\mu - \sigma<X<\mu + \sigma)}{2}\approx0.16$,$P(X\geq117.5)=P(X\geq\mu + \sigma)=\frac{1 - P(\mu - \sigma<X<\mu + \sigma)}{2}\approx0.16$,又成绩在117.5分以上(含117.5分)的学生有80人,所以高三考生总人数为$80÷0.16 = 500$(人)。因为$P(X>135)=P(x>\mu + 2\sigma)=\frac{1 - P(\mu - 2\sigma<X<\mu + 2\sigma)}{2}\approx0.02$,所以本次考试数学成绩特别优秀的大约有$500×0.02 = 10$(人)。]
查看更多完整答案,请扫码查看


