《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

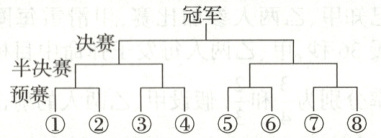
6. (2025·安徽合肥一中月考)有$A$，$B$，$C$，$D$，$E$，$F$，$G$，$H$八名运动员参加乒乓球赛事，该赛事采用预赛、半决赛和决赛三轮淘汰制决定最后的冠军(如图).八名运动员在比赛开始前抽签随机决定各自的位置编号，已知$B$～$H$这七名运动员互相对决时彼此间的获胜概率均为$\frac{1}{2}$，$A$运动员与其他运动员对决时，$A$获胜的概率为$\frac{2}{3}$，每场对决没有平局，且结果相互独立.

(1)求这八名运动员各自获得冠军的概率；
(2)求$B$与$A$对决过且最后获得冠军的概率；
(3)求$B$与$C$对决过且最后获得冠军的概率.

答案： 6.解：
(1)$A$夺冠即为三轮比赛都获胜，所以$A$夺冠的概率为$(\frac{2}{3})^3=\frac{8}{27}$.由题意，$B\sim H$七名运动员水平相同，且八名运动员各自夺冠概率之和为$1$，所以$B\sim H$七名运动员各自夺冠的概率均为$\frac{1}{7}×(1-\frac{8}{27})=\frac{19}{189}$.
(2)记事件$B=$“$B$获得冠军”，事件$A_i=$“$B$与$A$在第$i$轮对决”，$i=1,2,3$.不妨设$A$在①号位，则$B$在第$1,2,3$轮能与$A$对决时其位置编号分别为②,③④,⑤⑥⑦⑧.故$P(AB)=P((A_1+A_2+A_3)B)=P(A_1B)+P(A_2B)+P(A_3B)$，$P(A_1B)=\frac{1}{7}×(1-\frac{2}{3})×\frac{1}{2}×\frac{1}{84}$，$P(A_2B)=\frac{4}{7}×\frac{2}{3}×\frac{1}{2}×(1-\frac{2}{3})×\frac{1}{63}$，$P(A_3B)=\frac{4}{189}×\frac{1}{2}×\frac{1}{2}×(1-\frac{2}{3})=\frac{37}{756}$，所以$P(AB)=\frac{1}{84}+\frac{4}{63}+\frac{37}{189×3}=\frac{37}{189}$.
(3)记事件$C=$“$B$与$C$对决过”.$B$没有与$A$对决过且最后获得冠军的概率$P(\overline{A}B)=P(B)-P(AB)=\frac{19}{189}-\frac{37}{756}=\frac{39}{756}$，$P(BC)=P((A+\overline{A})BC)=P(ABC)+P(\overline{A}BC)=P(AB)P(C|AB)+P(\overline{A}B)P(C|\overline{A}B)$.由题意，$C\sim H$六名运动员与$B$对决过的概率相同，$B$夺冠时共与三名运动员对决过，所以$P(C|AB)=\frac{2}{6}$，$P(C|\overline{AB})=\frac{3}{6}$，代入得$P(BC)=\frac{37}{756}×\frac{2}{6}+\frac{39}{756}×\frac{3}{6}=\frac{191}{4536}$.

7. (2025·辽宁大连二十四中月考)某校开展“学习二十大，永远跟党走”网络知识竞赛.每人可参加多轮答题活动，每轮答题情况互不影响.每轮比赛共有两组题，每组都有两道题，只有第一组的两道题均答对，方可进行第二组答题，否则本轮答题结束.已知甲同学第一组每道题答对的概率均为$\frac{2}{3}$，第二组每道题答对的概率均为$\frac{1}{2}$，两组题至少答对 3 题才可获得一枚纪念章.
(1)记甲同学在一轮比赛中答对的题目数为$X$，请写出$X$的分布列，并求$E(X)$；
(2)若甲同学进行了 4 轮答题，求甲同学恰好获得 2 枚纪念章的概率.

答案： 7.解：
(1)由题意，$X$可取$0,1,2,3,4.P(X=0)=(1-\frac{2}{3})×(1-\frac{2}{3})=\frac{1}{9}$，$P(X=1)=C_{2}^{1}×\frac{2}{3}×(1-\frac{2}{3})=\frac{4}{9}$，$P(X=2)=\frac{2}{3}×\frac{2}{3}×(1-\frac{1}{2})×(1-\frac{1}{2})=\frac{1}{9}$，$P(X=3)=\frac{2}{3}×\frac{2}{3}× C_{2}^{1}×\frac{1}{2}×\frac{1}{2}=\frac{2}{9}$，$P(X=4)=\frac{2}{3}×\frac{2}{3}×\frac{1}{2}×\frac{1}{2}=\frac{1}{9}$，所以$X$的分布列为：
$X$ 0 1 2 3 4
$P$ $\frac{1}{9}$ $\frac{4}{9}$ $\frac{1}{9}$ $\frac{2}{9}$ $\frac{1}{9}$
故$E(X)=0×\frac{1}{9}+1×\frac{4}{9}+2×\frac{1}{9}+3×\frac{2}{9}+4×\frac{1}{9}=\frac{16}{9}$.
(2)每一轮获得纪念章的概率为$P=P(X=3)+P(X=4)=\frac{1}{9}+\frac{1}{9}=\frac{2}{9}$，设$4$轮答题获得纪念章的数量为$Y$，则$Y\sim B(4,\frac{1}{3})$，$P(Y=2)=C_{4}^{2}(\frac{1}{3})^{2}×(\frac{2}{3})^{4-2}=\frac{8}{27}$，即甲同学恰好获得$2$枚纪念章的概率是$\frac{8}{27}$.

8. (2025·山东济宁一中月考)某公司招聘考试分笔试与面试两部分进行，每部分成绩只记“合格”与“不合格”，两部分成绩都合格者被公司录取.甲、乙、丙三人在笔试部分合格的概率分别为$\frac{3}{4}$，$\frac{2}{3}$，$\frac{2}{3}$，在面试部分合格的概率分别为$\frac{3}{4}$，$\frac{3}{4}$，$\frac{5}{6}$，所有考试是否合格相互之间没有影响.已知甲、乙、丙三人都同时参加了笔试和面试.
(1)在甲、乙、丙三人中，谁被录取的可能性最大？
(2)设甲、乙、丙三人中被录取的人数为$X$，求$X$的分布列和期望.

答案： 8.解：
(1)甲被录取的概率为$P_1=(\frac{3}{4})^2=\frac{9}{16}$，乙被录取的概率为$P_2=\frac{2}{3}×\frac{3}{4}=\frac{1}{2}$，丙被录取的概率为$P_3=\frac{2}{3}×\frac{5}{6}×\frac{5}{9}$，因为$\frac{9}{16}＞\frac{5}{9}＞\frac{1}{2}$，所以甲被录取的可能性最大.
(2)由题意知，随机变量$X$的所有可能取值为$0,1,2,3,P(X=0)=\frac{7}{16}×\frac{1}{2}×\frac{4}{9}=\frac{7}{72}$，$P(X=3)=\frac{9}{16}×\frac{1}{2}×\frac{5}{9}=\frac{5}{32}$，$P(X=1)=\frac{9}{16}×\frac{1}{2}×\frac{4}{9}+\frac{7}{16}×\frac{1}{2}×\frac{5}{9}=\frac{11}{32}$，$P(X=2)=1-P(X=0)-P(X=1)-P(X=3)=\frac{29}{72}$，所以$X$的分布列为：
$X$ 0 1 2 3
$P$ $\frac{7}{72}$ $\frac{11}{32}$ $\frac{29}{72}$ $\frac{5}{32}$
故期望$E(X)=0×\frac{7}{72}+1×\frac{11}{32}+2×\frac{29}{72}+3×\frac{5}{32}=\frac{233}{144}$.