《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

8. (经典·新高考全国Ⅰ)甲、乙两人投篮，每次由其中一人投篮，规则如下：若命中则此人继续投篮，若未命中则换为对方投篮.无论之前投篮情况如何，甲每次投篮的命中率均为$0.6$，乙每次投篮的命中率均为$0.8$.由抽签确定第1次投篮的人选，第1次投篮的人是甲、乙的概率各为$0.5$.
(1)求第2次投篮的人是乙的概率.
(2)求第$i$次投篮的人是甲的概率.
(3)已知：若随机变量$X_{i}$服从两点分布，且$P(X_{i}=1)=1-P(X_{i}=0)=q_{i},i=1,2,·s,n$，则$E(\sum_{i = 1}^{n}X_{i})=\sum_{i = 1}^{n}q_{i}$.记前$n$次(即从第1次到第$n$次投篮)中甲投篮的次数为$Y$，求$E(Y)$.

答案：
(1) 第2次投篮的人是乙的情况为：第1次甲投未中（换乙）或第1次乙投命中（继续乙）。
第1次甲投概率0.5，未命中概率0.4，贡献概率$0.5×0.4=0.2$；
第1次乙投概率0.5，命中概率0.8，贡献概率$0.5×0.8=0.4$；
故第2次投篮的人是乙的概率为$0.2+0.4=0.6$。
(2) 设第$i$次投篮的人是甲的概率为$p_i$。
$i=1$时，$p_1=0.5$。
对$i≥2$，$p_i=$第$i-1$次甲投命中概率+第$i-1$次乙投未命中概率，即$p_i=0.6p_{i-1}+0.2(1-p_{i-1})=0.4p_{i-1}+0.2$。
递推式变形为$p_i-\frac{1}{3}=0.4(p_{i-1}-\frac{1}{3})$，首项$p_1-\frac{1}{3}=\frac{1}{6}$，
故$p_i=\frac{1}{3}+\frac{1}{6}(0.4)^{i-1}$。
(3) $Y=\sum_{i=1}^n X_i$，$E(Y)=\sum_{i=1}^n E(X_i)=\sum_{i=1}^n p_i$。
由
(2)，$p_i=\frac{1}{3}+\frac{1}{6}(0.4)^{i-1}$，
则$E(Y)=\sum_{i=1}^n\left[\frac{1}{3}+\frac{1}{6}(0.4)^{i-1}\right]=\frac{n}{3}+\frac{1}{6}·\frac{1-(0.4)^n}{1-0.4}=\frac{n}{3}+\frac{5(1-0.4^n)}{18}$。
答案
(1) $\boxed{0.6}$
(2) $\boxed{p_i=\frac{1}{3}+\frac{1}{6}(0.4)^{i-1}}$
(3) $\boxed{E(Y)=\frac{n}{3}+\frac{5(1-0.4^n)}{18}}$

9. (经典·新高考全国Ⅱ)某物理量的测量结果服从正态分布$N(10,\sigma^{2})$，下列结论中不正确的是

A.$\sigma$越小，该物理量在一次测量中在$(9.9,10.1)$的概率越大
B.该物理量在一次测量中大于10的概率为$0.5$
C.该物理量在一次测量中小于$9.99$与大于$10.01$的概率相等
D.该物理量在一次测量中落在$(9.9,10.2)$与落在$(10,10.3)$的概率相等

答案： 9.D

10. (2024·全国Ⅰ)[多选]随着“一带一路”国际合作的深入，某茶叶种植区多措并举推动茶叶出口.为了解推动出口后的亩收入(单位：万元)情况，从该种植区抽取样本，得到推动出口后亩收入的样本均值$\overline{x}=2.1$，样本方差$s^{2}=0.01$.已知该种植区以往的亩收入$X$服从正态分布$N(1.8,0.1^{2})$，假设推动出口后的亩收入$Y$服从正态分布$N(\overline{x},s^{2})$，则(若随机变量$Z$服从正态分布$N(\mu,\sigma^{2})$，则$P(Z＜\mu+\sigma)\approx0.8413$)

A.$P(X＞2)＞0.2$
B.$P(X＞2)＜0.5$
C.$P(Y＞2)＞0.5$
D.$P(Y＞2)＜0.8$

答案： 10.

11. (经典·湖北)设$X\sim N(\mu_{1},\sigma_{1}^{2})$，$Y\sim N(\mu_{2},\sigma_{2}^{2})$，这两个正态密度曲线如图所示，下列结论中正确的是


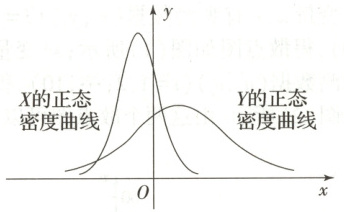
A.$P(Y\geq\mu_{2})\geq P(Y\geq\mu_{1})$
B.$P(X\leq\sigma_{2})\leq P(X\leq\sigma_{1})$
C.对任意正数$t$，$P(X\leq t)\geq P(Y\leq t)$
D.对任意正数$t$，$P(X\geq t)\geq P(Y\geq t)$

答案： 11.C

12. (经典·新高考全国Ⅱ)已知随机变量$X$服从正态分布$N(2,\sigma^{2})$，且$P(2＜X\leq2.5)=0.36$，则$P(X＞2.5)=$_.0.14

答案： 12.0.14[提示：]