《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

7.【题型二、三】(2025·广西钦州一中高二下月考)某袋中装有大小相同、质地均匀的黑球和白球共 5 个。从袋中随机取出 3 个球，已知不全为黑球的概率为 $\frac{9}{10}$，若记取出 3 个球中黑球的个数为 $X$，则 $D(X)=$$\frac{9}{25}$。

答案： 7.$\frac{9}{25}$[提示：设袋中黑球个数为$x$，则白球个数为$(5 - x)$，所以
$1 - \frac{C_{3}^{3}}{C_{10}^{3}} = \frac{9}{10}$，所以$x = 3$，所以$X$的可能取值为1,2,3,$P(X = 1)$
$ = \frac{C_{3}^{1}C_{2}^{2}}{C_{5}^{3}} = \frac{3}{10}$,$P(X = 2) = \frac{C_{3}^{2}C_{2}^{1}}{C_{5}^{3}} = \frac{3}{5}$,$P(X = 3) = \frac{C_{3}^{3}}{C_{5}^{3}} = \frac{1}{10}$,故
$E(X) = 1 × \frac{3}{10} + 2 × \frac{3}{5} + 3 × \frac{1}{10} = \frac{9}{5}$,$D(X) = (1 - \frac{9}{5})^{2} × \frac{3}{10} +$
$(2 - \frac{9}{5})^{2} × \frac{3}{5} + (3 - \frac{9}{5})^{2} × \frac{1}{10} = \frac{9}{25}$.]

8.【题型二、三】（2025·安徽芜湖高二下期末）某校将开展“古诗词”知识竞赛，经过层层筛选，还有最后一个参赛名额要在甲、乙两名学生中产生。现准备了 6 个不同问题进行测试，甲、乙两名学生都能正确回答其中的 4 个问题，且甲、乙两名学生对每个问题回答正确与否都相互独立。评委会设计了两种测试方案：
方案一：从装有 6 个不同问题的纸盒中依次有放回地抽取 4 个问题作答；
方案二：从装有 6 个不同问题的纸盒中依次不放回地抽取 4 个问题作答。
假设甲同学选择方案一，乙同学选择方案二。
（1）求乙同学答对问题个数的分布列和均值。
（2）若测试过程中答对 1 个问题得 2 分，答错扣 1 分。你认为哪位学生得分高？哪位学生发挥更稳定？请说明理由。

答案： 8.解：
(1)设乙同学答对问题的个数为$X$，由题意可知随机变量$X$的可能取值有2,3,4，$P(X = 2) = \frac{C_{4}^{2}C_{2}^{2}}{C_{6}^{4}} = \frac{2}{5}$,$P(X = 3) = \frac{C_{4}^{3}C_{2}^{1}}{C_{6}^{4}} =$
$\frac{8}{15}$,$P(X = 4) = \frac{C_{4}^{4}}{C_{6}^{4}} = \frac{1}{15}$，所以随机变量$X$的分布列为：
$X$ 2 3 4
$P$ $\frac{2}{5}$ $\frac{8}{15}$ $\frac{1}{15}$
所以$E(X) = 2 × \frac{2}{5} + 3 × \frac{8}{15} + 4 × \frac{1}{15} = \frac{8}{3}$.
(2)设甲同学答对问题的个数为$Y$，则$Y \sim B(4,\frac{2}{3})$，由二项分布的期望和方差公式得$E(Y) = 4 × \frac{2}{3} = \frac{8}{3}$,$D(Y) = 4 × \frac{2}{3} × \frac{1}{3} = \frac{8}{9}$.甲回答问题得分为$2Y - (4 - Y) = 3Y - 4$，所以甲得分的均值为$E(3Y - 4) = 3E(Y) - 4 = 3 × \frac{8}{3} - 4 = 4$，方差为$D(3Y - 4) = 9D(Y) = 9 × \frac{8}{9} =$
$\frac{16}{5}$.
由
(1)知$E(X) = \frac{8}{3}$,$D(X) = (2 - \frac{8}{3})^{2} × \frac{2}{5} +$
$(3 - \frac{8}{3})^{2} × \frac{8}{15} + (4 - \frac{8}{3})^{2} × \frac{1}{15} = \frac{16}{45}$，所以乙同学回答问题得分为$2X - (4 - X) = 3X - 4$，所以乙得分的均值为$E(3X - 4) =$
$3E(X) - 4 = 3 × \frac{8}{3} - 4 = 4$，方差为$D(3X - 4) = 9D(X) = 9 × \frac{16}{45} =$
$\frac{16}{5}$.
因为$E(3X - 4) = E(3Y - 4)$,$D(3X - 4) ＜ D(3Y - 4)$，所以甲、乙得分相同，但乙发挥更为稳定.

9.【题型二、三】（2025·辽宁抚顺雷锋中学高二下月考）某校为了参加市里举办的足球联赛，从学校的足球队中选出了水平较高的 18 人组成了代表队参加比赛，已知这 18 名队员来自高二年级的 4 个班级，每班对应的人数如下表所示：

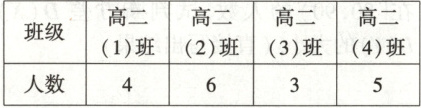
（1）从这 18 名队员中随机选出两人，求这两人来自同一个班级的概率；
（2）经过队员们的奋力拼搏，获得了这次联赛的冠军，若要从这 18 人中选出两人作为球员代表发言，设选出的两人中来自高二（1）班的人数为 $X$，求 $X$ 的分布列。

答案： 9.解：
(1)设事件$A$为“从这18名队员中随机选出两人，这两人来自同一个班级”，则$P(A) = \frac{C_{6}^{2} + C_{6}^{2} + C_{3}^{2} + C_{3}^{2}}{C_{18}^{2}} =$
$\frac{6 + 15 + 3 + 10}{153} = \frac{2}{9}$.
(2)由题意可知$X$的所有可能取值为
0,1,2，且服从超几何分布，故$P(X = 0) = \frac{C_{12}^{2}C_{6}^{0}}{C_{18}^{2}} = \frac{91}{153}$，$P(X = 1) =$
$\frac{C_{12}^{1}C_{6}^{1}}{C_{18}^{2}} = \frac{56}{153}$,$P(X = 2) = \frac{C_{12}^{0}C_{6}^{2}}{C_{18}^{2}} = \frac{2}{51}$，所以$X$的分布列为：
$X$ 0 1 2
$P$ $\frac{91}{153}$ $\frac{56}{153}$ $\frac{2}{51}$