2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
8. (2025·湖北襄阳五中高三下适应性考试)若随机变量$\xi$的分布列如下表,表中数列$\{ a_{n}\}$为等差数列,则$P(\xi = 5)$的值是(

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$
D
)
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$
答案:
8.D[提示:由分布列的性质可知,$a_1+a_2+a_3+a_4+a_5=1$,再根据数列{$a_n$}为等差数列,得$5a_3=1$,即$a_3=\frac{1}{5}$,故$P(ξ=5)=\frac{1}{5}$.]
9. (教材改编题)设随机变量$X$的分布列如下表:

则$P(X\geq 3)=$

则$P(X\geq 3)=$
0.7
。
答案:
9.0.7[提示:由题意可得$k+2k+3k+4k=1$,解得$k=0.1$,所以$P(X\geq3)=P(X=3)+P(X=4)=0.3+0.4=0.7$.]
10. 已知$X$服从两点分布,且$P(X = 1) = 0.3$。
(1)求$P(X = 0)$;
(2)若$Y = 2X + 1$,写出$Y$的分布列。
(1)求$P(X = 0)$;
(2)若$Y = 2X + 1$,写出$Y$的分布列。
答案:
10.解:
(1)$P(X=0)=1-0.3=0.7$.
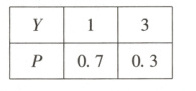
(2)当$X=0$时,$Y=1$;当$X=1$时,$Y=3$.所以$Y$的分布列为:
10.解:
(1)$P(X=0)=1-0.3=0.7$.
(2)当$X=0$时,$Y=1$;当$X=1$时,$Y=3$.所以$Y$的分布列为:

11. (教材改编题)袋内有10个红球,5个白球,从中摸出2个球,记$X=\begin{cases}0,两球全是白球,\\1,两球不全是白球,\end{cases}$求$X$的分布列。
答案:
11.解:由题意知$X$服从两点分布,且$P(X=0)=\frac{C_5^2}{C_{15}^2}=\frac{2}{21}$,$P(X=1)=1-P(X=0)=\frac{19}{21}$.所以$X$的分布列为:
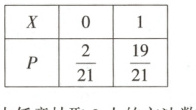
11.解:由题意知$X$服从两点分布,且$P(X=0)=\frac{C_5^2}{C_{15}^2}=\frac{2}{21}$,$P(X=1)=1-P(X=0)=\frac{19}{21}$.所以$X$的分布列为:

12. 4月23日是“世界读书日”,学校开展了一系列的读书教育活动。学校为了解高二学生课外阅读情况,从高二某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生中抽取12名学生参加问卷调查。各组人数统计如下:
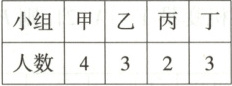
(1)从参加问卷调查的12名学生中随机抽取2人,求这2人来自同一个小组的概率;
(2)从已抽取的甲、丙两个小组的学生中随机抽取2人,用$X$表示抽得甲组学生的人数,求随机变量$X$的分布列。

(1)从参加问卷调查的12名学生中随机抽取2人,求这2人来自同一个小组的概率;
(2)从已抽取的甲、丙两个小组的学生中随机抽取2人,用$X$表示抽得甲组学生的人数,求随机变量$X$的分布列。
答案:
12.解:
(1)从12人中任意抽取2人的方法数为$C_{12}^2=\frac{12×11}{2}=66$,由题意知,甲、乙、丙、丁四个小组中抽取的人数分别为4,3,2,3,2人来自同一组的方法数为$C_4^2+C_3^2+C_2^2+C_3^2=13$,所以所求概率为$\frac{13}{66}$.
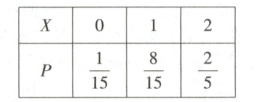
(2)随机变量$X$的取值可以为0,1,2,$P(X=0)=\frac{C_6^2}{C_6^2}=\frac{1}{15}$,$P(X=1)=\frac{C_4^1C_1^1}{C_6^2}=\frac{8}{15}$,$P(X=2)=\frac{C_4^2}{C_6^2}=\frac{2}{5}$.所以$X$的分布列为:
12.解:
(1)从12人中任意抽取2人的方法数为$C_{12}^2=\frac{12×11}{2}=66$,由题意知,甲、乙、丙、丁四个小组中抽取的人数分别为4,3,2,3,2人来自同一组的方法数为$C_4^2+C_3^2+C_2^2+C_3^2=13$,所以所求概率为$\frac{13}{66}$.
(2)随机变量$X$的取值可以为0,1,2,$P(X=0)=\frac{C_6^2}{C_6^2}=\frac{1}{15}$,$P(X=1)=\frac{C_4^1C_1^1}{C_6^2}=\frac{8}{15}$,$P(X=2)=\frac{C_4^2}{C_6^2}=\frac{2}{5}$.所以$X$的分布列为:

1. 【题型一】下面给出四个随机变量:
①一高速公路上某收费站在半小时内经过的车辆数$\xi$;
②一个沿直线$y = 2x$进行随机运动的质点,它在该直线上的位置$\eta$;
③某指挥台5分钟内接到的雷达电话次数$X$;
④某同学离开哈尔滨市第三中学的距离$Y$。
其中是离散型随机变量的为(
A.①②
B.③④
C.①③
D.②④
①一高速公路上某收费站在半小时内经过的车辆数$\xi$;
②一个沿直线$y = 2x$进行随机运动的质点,它在该直线上的位置$\eta$;
③某指挥台5分钟内接到的雷达电话次数$X$;
④某同学离开哈尔滨市第三中学的距离$Y$。
其中是离散型随机变量的为(
C
)A.①②
B.③④
C.①③
D.②④
答案:
1.C[提示:对于①,半小时内经过的车辆数可以一一列举出来,①是离散型随机变量;对于②,沿直线y=2x进行机械运动的质点,质点在直线上的位置不能一一列举出来,②不是离散型随机变量;对于③,5分钟内接到的雷达电话次数可以一一列举出来,③是离散型随机变量;对于④,某同学离开哈尔滨市第三中学的距离可为某一区间内的任意值,不能一一列举出来,④不是离散型随机变量.所以给定的随机变量是离散型随机变量的有①③.]
查看更多完整答案,请扫码查看


