2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
7. 甲、乙两人进行射击比赛,各射击 4 局,每局射击 10 次,射击命中目标得 1 分,未命中目标得 0 分,两人 4 局的得分情况如下表:

(1) 若从甲的 4 局比赛中随机选取 2 局,求这 2 局的得分恰好相等的概率。
(2) 如果 $ x = y = 7 $,从甲、乙两人的 4 局比赛中随机各选取 1 局,记这 2 局的得分和为 $ X $,求 $ X $ 的分布列和数学期望。

(1) 若从甲的 4 局比赛中随机选取 2 局,求这 2 局的得分恰好相等的概率。
(2) 如果 $ x = y = 7 $,从甲、乙两人的 4 局比赛中随机各选取 1 局,记这 2 局的得分和为 $ X $,求 $ X $ 的分布列和数学期望。
答案:
7.解:
(1)从甲的$4$局比赛中随机选取$2$局的情况有$C_{4}^{2}=6$种,得分恰好相等的有$2$种,所以这$2$局的得分恰好相等的概率为$\frac{2}{6}=\frac{1}{3}$.
(2)当$x=y=7$时,$X$的可能取值有$13,15,16,18$,且$P(X=13)=\frac{C_{2}^{1}C_{3}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{3}{8},P(X=15)=\frac{C_{1}^{1}C_{4}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{1}{8}$,
$P(X=16)=\frac{C_{2}^{1}C_{3}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{3}{8},P(X=18)=\frac{C_{2}^{1}C_{1}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{1}{8}$,所以$X$的分布列为:
$E(X)=13 × \frac{3}{8}+15 × \frac{1}{8}+16 × \frac{3}{8}+18 × \frac{1}{8}=15$.
7.解:
(1)从甲的$4$局比赛中随机选取$2$局的情况有$C_{4}^{2}=6$种,得分恰好相等的有$2$种,所以这$2$局的得分恰好相等的概率为$\frac{2}{6}=\frac{1}{3}$.
(2)当$x=y=7$时,$X$的可能取值有$13,15,16,18$,且$P(X=13)=\frac{C_{2}^{1}C_{3}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{3}{8},P(X=15)=\frac{C_{1}^{1}C_{4}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{1}{8}$,
$P(X=16)=\frac{C_{2}^{1}C_{3}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{3}{8},P(X=18)=\frac{C_{2}^{1}C_{1}^{1}}{C_{4}^{1}C_{4}^{1}}=\frac{1}{8}$,所以$X$的分布列为:

$E(X)=13 × \frac{3}{8}+15 × \frac{1}{8}+16 × \frac{3}{8}+18 × \frac{1}{8}=15$.
8. (2025·辽宁葫芦岛一中高三模拟改编) 为了培养具有创新潜质的学生,某高校决定选拔优秀的中学生参加人工智能冬令营。选拔考试分为“Python 编程语言”和“数据结构算法”两个科目,考生两个科目考试的顺序自选,若第一科考试不合格,则淘汰;若第一科考试合格则进行第二科考试,无论第二科是否合格,考试都结束。“Python 编程语言”考试合格得 4 分,否则得 0 分;“数据结构算法”考试合格得 6 分,否则得 0 分。
已知甲同学参加“Python 编程语言”考试合格的概率为 0.8,参加“数据结构算法”考试合格的概率为 0.7。
(1) 若甲同学先进行“Python 编程语言”考试,记 $ X $ 为甲同学的累计得分,求 $ X $ 的分布列;
(2) 为使累计得分的期望最大,甲同学应选择先进行哪类考试? 并说明理由。
已知甲同学参加“Python 编程语言”考试合格的概率为 0.8,参加“数据结构算法”考试合格的概率为 0.7。
(1) 若甲同学先进行“Python 编程语言”考试,记 $ X $ 为甲同学的累计得分,求 $ X $ 的分布列;
(2) 为使累计得分的期望最大,甲同学应选择先进行哪类考试? 并说明理由。
答案:
8.解:
(1)由题意$X$的所有可能取值为$0,4,10$,所以$P(X=0)=1-0.8=0.2,P(X=4)=0.8 × (1-0.7)=0.24,P(X=10)=0.8 × 0.7=0.56$,所以$X$的分布列为:
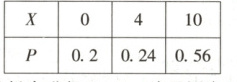
(2)甲同学应选择先进行“Python编程语言”考试,理由如下:由
(1)可知$E(X)=0 × 0.2+4 × 0.24+10 × 0.56=6.56$.若甲同学先进行“数据结构算法”考试,记$Y$为甲同学的累计得分,则$Y$的所有可能取值为$0,6,10,P(Y=0)=1-0.7=0.3,P(Y=6)=0.7 × (1-0.8)=0.14,P(Y=10)=0.7 × 0.8=0.56$,所以$Y$的分布列为:
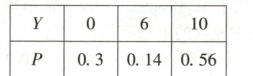
所以$E(Y)=0 × 0.3+6 × 0.14+10 × 0.56=6.44$,所以$E(X)>E(Y)$,所以甲同学应选择先进行“Python编程语言”考试.
8.解:
(1)由题意$X$的所有可能取值为$0,4,10$,所以$P(X=0)=1-0.8=0.2,P(X=4)=0.8 × (1-0.7)=0.24,P(X=10)=0.8 × 0.7=0.56$,所以$X$的分布列为:

(2)甲同学应选择先进行“Python编程语言”考试,理由如下:由
(1)可知$E(X)=0 × 0.2+4 × 0.24+10 × 0.56=6.56$.若甲同学先进行“数据结构算法”考试,记$Y$为甲同学的累计得分,则$Y$的所有可能取值为$0,6,10,P(Y=0)=1-0.7=0.3,P(Y=6)=0.7 × (1-0.8)=0.14,P(Y=10)=0.7 × 0.8=0.56$,所以$Y$的分布列为:

所以$E(Y)=0 × 0.3+6 × 0.14+10 × 0.56=6.44$,所以$E(X)>E(Y)$,所以甲同学应选择先进行“Python编程语言”考试.
1. 【题型一】某射手射击所得环数 $ \xi $ 的分布列如下表,已知 $ \xi $ 的数学期望 $ E(\xi)=8.9 $,则 $ y $ 的值为 (

A.0.2
B.0.5
C.0.4
D.0.3
C
)
A.0.2
B.0.5
C.0.4
D.0.3
答案:
1.C[提示:$\because \xi$的数学期望$E(\xi)=8.9,\therefore$由对手射击所得环数$\xi$的分布列,得$\begin{cases}x+0.1+0.3+y=1,\\7x+0.8+2.7+10y=8.9,\end{cases}$解得$\begin{cases}x=0.2,\\y=0.4.\end{cases}$]
2. 【题型一】(2025·山东青岛二中月考) [多选] 已知离散型随机变量 $ X $ 的分布列如下表所示,则 (

A.$ q = \frac{1}{3} $
B.$ q = \frac{1}{6} $
C.$ E(X)=4 $
D.$ E(2 - 3X)=10 $
BC
)
A.$ q = \frac{1}{3} $
B.$ q = \frac{1}{6} $
C.$ E(X)=4 $
D.$ E(2 - 3X)=10 $
答案:
2.BC[提示:由离散型随机变量分布列的性质可得$\frac{1}{2}+q+2q=1$,解得$q=\frac{1}{6}$,故A错误,B正确;由期望公式可得$E(X)=2 × \frac{1}{2}+4 × \frac{1}{6}+7 × \frac{1}{3}=4$,故C正确;$E(2-3X)=2-3E(X)=2-10,D$错误.]
3. 【题型一】(2025·吉林长春二中月考) [多选] 已知随机变量 $ X $ 的分布列为:

下列结论正确的是 (
A.$ m = \frac{5}{12} $
B.$ E(X)=\frac{9}{4} $
C.$ E(X + 2)=\frac{17}{4} $
D.$ E(2X)=9 $

下列结论正确的是 (
ABC
)A.$ m = \frac{5}{12} $
B.$ E(X)=\frac{9}{4} $
C.$ E(X + 2)=\frac{17}{4} $
D.$ E(2X)=9 $
答案:
3.ABC[提示:由$\frac{1}{6}+m+\frac{5}{12}=1$,得$m=\frac{5}{12}$,故A正确;$E(X)=1 × \frac{1}{6}+2 × \frac{5}{12}+3 × \frac{5}{12}=\frac{9}{4}$,故B正确;$E(X+2)=E(X)+2=\frac{17}{4}$,故C正确;$E(2X)=2E(X)=\frac{9}{2}$,故D错误.]
查看更多完整答案,请扫码查看


