2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. 【题型一】已知随机变量 $ X $ 的期望 $ E(X) = 0 $,方差 $ D(X) = 1 $,随机变量 $ Y = 2X - 1 $,则下列结论正确的是(
A.$ E(Y) = -1,D(Y) = 3 $
B.$ E(Y) = 1,D(Y) = 3 $
C.$ E(Y) = -1,D(Y) = 4 $
D.$ E(Y) = 1,D(Y) = 4 $
C
)A.$ E(Y) = -1,D(Y) = 3 $
B.$ E(Y) = 1,D(Y) = 3 $
C.$ E(Y) = -1,D(Y) = 4 $
D.$ E(Y) = 1,D(Y) = 4 $
答案:
1.C[提示:因为随机变量$X$的期望$E(X)=0$,方差$D(X)=1$,
又$Y = 2X - 1$,所以$E(Y)=E(2X - 1)=2E(X)-1=-1$,$D(Y)=$
$D(2X - 1)=2^{2}D(X)=4$.]
又$Y = 2X - 1$,所以$E(Y)=E(2X - 1)=2E(X)-1=-1$,$D(Y)=$
$D(2X - 1)=2^{2}D(X)=4$.]
2. 【题型一】[ 多选 ] 设 $ 0 < p < 1 $,已知随机变量 $ \xi $ 的分布列如下表,则下列结论正确的是(
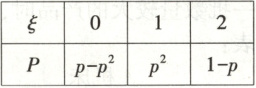
A.$ P(\xi = 0) < P(\xi = 2) $
B.$ P(\xi = 2) $ 的值最大
C.$ E(\xi) $ 随着 $ p $ 的增大而增大
D.当 $ p = \frac{1}{2} $ 时,$ D(\xi) = \frac{11}{16} $
AD
)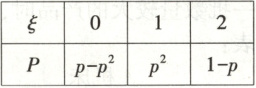
A.$ P(\xi = 0) < P(\xi = 2) $
B.$ P(\xi = 2) $ 的值最大
C.$ E(\xi) $ 随着 $ p $ 的增大而增大
D.当 $ p = \frac{1}{2} $ 时,$ D(\xi) = \frac{11}{16} $
答案:
2.AD[提示:$P(\xi = 0)=p - p^{2}=p(1 - p)<1 - p = P(\xi = 2)$,所以$A$
正确;令$p = \frac{3}{4}$,则$P(\xi = 2)=\frac{1}{4}$,$P(\xi = 1)=(\frac{3}{4})^{2}=\frac{9}{16}>$
$\frac{1}{4}$,所以$B$错误;由题意得$E(\xi)=p^{2}+2(1 - p)=(p - 1)^{2}+1$,
因为$0 < p < 1$,所以$E(\xi)$随着$p$的增大而减小,所以$C$错误;
当$p = \frac{1}{2}$时,$E(\xi)=1 × (\frac{1}{2})^{2}+\frac{1}{2}=\frac{5}{4}$,$D(\xi)=(0 - \frac{5}{4})^{2} ×$
$\frac{1}{4}+(1 - \frac{5}{4})^{2} × \frac{1}{4}+(2 - \frac{5}{4})^{2} × \frac{1}{2}=\frac{11}{16}$,所以$D$正确.]
正确;令$p = \frac{3}{4}$,则$P(\xi = 2)=\frac{1}{4}$,$P(\xi = 1)=(\frac{3}{4})^{2}=\frac{9}{16}>$
$\frac{1}{4}$,所以$B$错误;由题意得$E(\xi)=p^{2}+2(1 - p)=(p - 1)^{2}+1$,
因为$0 < p < 1$,所以$E(\xi)$随着$p$的增大而减小,所以$C$错误;
当$p = \frac{1}{2}$时,$E(\xi)=1 × (\frac{1}{2})^{2}+\frac{1}{2}=\frac{5}{4}$,$D(\xi)=(0 - \frac{5}{4})^{2} ×$
$\frac{1}{4}+(1 - \frac{5}{4})^{2} × \frac{1}{4}+(2 - \frac{5}{4})^{2} × \frac{1}{2}=\frac{11}{16}$,所以$D$正确.]
3. 【题型一】(2025·河南郑州一中高二下月考)[ 多选 ] 已知样本数据 $ x_1,x_2,·s,x_5 $ 的平均数是 3,方差是 2,样本数据 $ y_1,y_2,·s,y_5 $ 的平均数是 1,方差是 4,则下列结论正确的是(
A.数据 $ 2x_1 + 1,2x_2 + 1,·s,2x_5 + 1 $ 的平均数是 7
B.数据 $ 2y_1 - 1,2y_2 - 1,·s,2y_5 - 1 $ 的方差是 16
C.数据 $ x_1,x_2,·s,x_5,y_1,y_2,·s,y_5 $ 的平均数为 3
D.数据 $ x_1,x_2,·s,x_5,y_1,y_2,·s,y_5 $ 的方差为 4
ABD
)A.数据 $ 2x_1 + 1,2x_2 + 1,·s,2x_5 + 1 $ 的平均数是 7
B.数据 $ 2y_1 - 1,2y_2 - 1,·s,2y_5 - 1 $ 的方差是 16
C.数据 $ x_1,x_2,·s,x_5,y_1,y_2,·s,y_5 $ 的平均数为 3
D.数据 $ x_1,x_2,·s,x_5,y_1,y_2,·s,y_5 $ 的方差为 4
答案:
3.ABD[提示:由题意,$E(X)=3$,$D(X)=2$,$E(Y)=4$,对于$A$,由题设,数据平均数为$E(2X + 1)=2E(X)+1 = 7$,
正确;对于$B$,由题设,数据方差为$D(2Y - 1)=4D(Y)=16$,
正确;对于$C$,由题设,数据平均数为$\frac{5E(X)+5E(Y)}{10}=\frac{20}{10}=$
$2$,错误;对于$D$,由题设,数据方差为$\frac{5}{10}[D(X)+(E(X)-$
$2)^{2}]+ \frac{5}{10}[D(Y)+(E(Y)-2)^{2}]=\frac{1}{2}[2+(3 - 2)^{2}]+\frac{1}{2}[4+(1$
$-2)^{2}]=4$,正确.]
正确;对于$B$,由题设,数据方差为$D(2Y - 1)=4D(Y)=16$,
正确;对于$C$,由题设,数据平均数为$\frac{5E(X)+5E(Y)}{10}=\frac{20}{10}=$
$2$,错误;对于$D$,由题设,数据方差为$\frac{5}{10}[D(X)+(E(X)-$
$2)^{2}]+ \frac{5}{10}[D(Y)+(E(Y)-2)^{2}]=\frac{1}{2}[2+(3 - 2)^{2}]+\frac{1}{2}[4+(1$
$-2)^{2}]=4$,正确.]
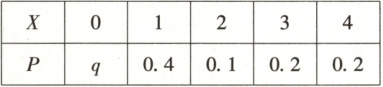
4. 【题型一】(2025·黑龙江牡丹江三中高二下期中)[ 多选 ] 设离散型随机变量 $ X $ 的分布列为:
若离散型随机变量 $ Y $ 满足 $ Y = 3X + 1 $,则下列结果正确的有(
A.$ q = 0.1 $
B.$ E(X) = 2,D(X) = 1.4 $
C.$ E(X) = 2,D(X) = 1.8 $
D.$ E(Y) = 7,D(Y) = 16.2 $
若离散型随机变量 $ Y $ 满足 $ Y = 3X + 1 $,则下列结果正确的有(
ACD
)
A.$ q = 0.1 $
B.$ E(X) = 2,D(X) = 1.4 $
C.$ E(X) = 2,D(X) = 1.8 $
D.$ E(Y) = 7,D(Y) = 16.2 $
答案:
4.ACD[提示:由$q + 0.4 + 0.1 + 0.2 + 0.2 = 1$,可得$q = 0.1$,故$A$
正确;$E(X)=0 × 0.1 + 1 × 0.4 + 2 × 0.1 + 3 × 0.2 + 4 × 0.2 = 2$,
$D(X)=(0 - 2)^{2} × 0.1+(1 - 2)^{2} × 0.4+(2 - 2)^{2} × 0.1+(3 - 2)^{2} ×$
$0.2+(4 - 2)^{2} × 0.2 = 1.8$,故$B$错误,$C$正确;$E(Y)=3E(X)+$
$1 = 3 × 2+1 = 7$,$D(Y)=3^{2}D(X)=3^{2} × 1.8 = 16.2$,故$D$正确.]
正确;$E(X)=0 × 0.1 + 1 × 0.4 + 2 × 0.1 + 3 × 0.2 + 4 × 0.2 = 2$,
$D(X)=(0 - 2)^{2} × 0.1+(1 - 2)^{2} × 0.4+(2 - 2)^{2} × 0.1+(3 - 2)^{2} ×$
$0.2+(4 - 2)^{2} × 0.2 = 1.8$,故$B$错误,$C$正确;$E(Y)=3E(X)+$
$1 = 3 × 2+1 = 7$,$D(Y)=3^{2}D(X)=3^{2} × 1.8 = 16.2$,故$D$正确.]
5. 【题型一】[ 多选 ] 若随机变量 $ X $ 服从两点分布,且 $ P(X = 0) = \frac{2}{3} $,则(
A.$ E(X) = \frac{1}{3} $
B.$ D(X) = \frac{2}{9} $
C.$ E(2X + 1) = \frac{7}{3} $
D.$ D(2X + 1) = \frac{13}{9} $
AB
)A.$ E(X) = \frac{1}{3} $
B.$ D(X) = \frac{2}{9} $
C.$ E(2X + 1) = \frac{7}{3} $
D.$ D(2X + 1) = \frac{13}{9} $
答案:
5.AB[提示:因为随机变量$X$服从两点分布,且$P(X = 0)=$
$\frac{2}{3}$,所以$P(X = 1)=\frac{1}{3}$,所以$E(X)=0 × \frac{2}{3}+1 × \frac{1}{3}=\frac{1}{3}$,故$A$
正确;$E(2X + 1)=2E(X)+1=\frac{5}{3}$,故$C$错误;$D(X)=$
$(0 - \frac{1}{3})^{2} × \frac{2}{3}+(1 - \frac{1}{3})^{2} × \frac{1}{3}=\frac{2}{9}$,故$B$正确;$D(2X + 1)=$
$4D(X)=\frac{8}{9}$,故$D$错误.]
$\frac{2}{3}$,所以$P(X = 1)=\frac{1}{3}$,所以$E(X)=0 × \frac{2}{3}+1 × \frac{1}{3}=\frac{1}{3}$,故$A$
正确;$E(2X + 1)=2E(X)+1=\frac{5}{3}$,故$C$错误;$D(X)=$
$(0 - \frac{1}{3})^{2} × \frac{2}{3}+(1 - \frac{1}{3})^{2} × \frac{1}{3}=\frac{2}{9}$,故$B$正确;$D(2X + 1)=$
$4D(X)=\frac{8}{9}$,故$D$错误.]
6. 【题型二、三】(2025·黑龙江大庆铁人高二下期中)[ 多选 ] 高考数学试题第二题为多选题,共 3 个小题,每小题有 4 个选项,其中有 2 个或 3 个是正确选项,全部选对得 6 分,部分选对得部分分,有选错的得 0 分. 若正确答案是 2 个选项,只选对 1 个得 3 分,有选错的得 0 分;若正确答案是 3 个选项,只选对 1 个得 2 分,只选对 2 个得 4 分,有选错的得 0 分. 小明对其中的一道题完全不会,该题有两个正确选项的概率是 $ \frac{1}{2} $,记 $ X $ 为小明随机选择 1 个选项的得分,记 $ Y $ 为小明随机选择 2 个选项的得分,则(
A.$ P(X = 3) = P(Y = 4) $
B.$ P(X = 0) > P(Y = 0) $
C.$ E(X) = E(Y) $
D.$ D(X) < D(Y) $
ACD
)A.$ P(X = 3) = P(Y = 4) $
B.$ P(X = 0) > P(Y = 0) $
C.$ E(X) = E(Y) $
D.$ D(X) < D(Y) $
答案:
6.ACD[提示:对于$A$,若$X = 3$,即该题有两个正确选项,小明
从正确选项中选择$1$个,所以$P(X = 3)=\frac{1}{2} × \frac{C_{2}^{1}}{C_{4}^{1}}=\frac{1}{4}$,若$Y =$
$4$,即该题有$3$个正确选项,小明从正确选项中选择$2$个,所
以$P(Y = 4)=\frac{1}{2} × \frac{C_{3}^{2}}{C_{4}^{2}}=\frac{1}{4}$.所以$P(X = 3)=P(Y = 4)=\frac{1}{4}$,故
$A$正确.对于$B$,当$X = 0$时,若该题有两个正确选项,则小明
从两个错误选项中选择$1$个,若该题有三个正确选项,则小明
选择错误选项,所以$P(X = 0)=\frac{1}{2} × \frac{C_{2}^{1}}{C_{4}^{1}}+\frac{1}{2} × \frac{C_{3}^{1}}{C_{8}^{1}}=\frac{3}{8}$;当$Y$
$=0$时,若该题有两个正确选项,则小明从两个错误选项中
选择$1$个,从两个正确选项中选择$1$个,或选择两个错误选
项,若该题有三个正确选项,则小明选择错误选项,再从$3$
个正确选项中选择$1$个,所以$P(Y = 0)=\frac{1}{2} × \frac{C_{2}^{2}+C_{2}^{1}C_{2}^{1}}{C_{4}^{2}} × \frac{C_{2}^{1}C_{2}^{1}}{C_{3}^{1}}+$
$\frac{1}{2} × \frac{C_{3}^{1}C_{4}^{2}+C_{3}^{0}C_{4}^{3}}{C_{7}^{3}} × \frac{C_{3}^{1}}{C_{3}^{1}}=\frac{2}{3}$.因为$\frac{2}{3}>\frac{3}{8}$,所以$P(X = 0)<P(Y = 0)$,故$B$错误.
对于$C$,$X$的可能取值为$0,2,3$,其中$X = 2$,表示该题有$3$
个正确选项,小明从正确选项中选择$1$个,所以$P(X = 2)=\frac{1}{2}$
$× \frac{C_{3}^{1}}{C_{4}^{1}} × \frac{C_{3}^{1}}{C_{8}^{1}}=\frac{3}{8}$,所以$E(X)=0 × \frac{3}{8}+2 × \frac{3}{8}+3 × \frac{1}{4}=\frac{3}{2}$.$Y$的可能取
值为$0,4,6$,其中$Y = 6$,表示该题有$2$个正确选项,小明选择
了$2$个正确选项,所以$P(Y = 6)=\frac{1}{2} × \frac{C_{2}^{2}}{C_{4}^{2}}=\frac{1}{12}$,所以$E(Y)=$
$0 × \frac{2}{3}+4 × \frac{1}{4}+6 × \frac{1}{12}=\frac{3}{2}$.所以$E(X)=E(Y)$,故$C$正确.对
于$D$,$D(X)=(0 - \frac{3}{2})^{2} × \frac{3}{8}+\frac{1}{4} × (2 - \frac{3}{2})^{2}+\frac{3}{8} × (3 - \frac{3}{2})^{2} × \frac{1}{4}=$
$\frac{9}{4} × \frac{3}{8} × \frac{1}{4}+\frac{1}{4} × \frac{1}{4}+\frac{3}{8} × \frac{9}{4} × \frac{1}{4}=\frac{9}{4} × \frac{3}{8} × \frac{1}{2}+\frac{25}{4} × \frac{1}{4}+\frac{81}{4} × \frac{1}{12}=$
$\frac{19}{4}$,所以$D(X)<D(Y)$,故$D$正确.]
从正确选项中选择$1$个,所以$P(X = 3)=\frac{1}{2} × \frac{C_{2}^{1}}{C_{4}^{1}}=\frac{1}{4}$,若$Y =$
$4$,即该题有$3$个正确选项,小明从正确选项中选择$2$个,所
以$P(Y = 4)=\frac{1}{2} × \frac{C_{3}^{2}}{C_{4}^{2}}=\frac{1}{4}$.所以$P(X = 3)=P(Y = 4)=\frac{1}{4}$,故
$A$正确.对于$B$,当$X = 0$时,若该题有两个正确选项,则小明
从两个错误选项中选择$1$个,若该题有三个正确选项,则小明
选择错误选项,所以$P(X = 0)=\frac{1}{2} × \frac{C_{2}^{1}}{C_{4}^{1}}+\frac{1}{2} × \frac{C_{3}^{1}}{C_{8}^{1}}=\frac{3}{8}$;当$Y$
$=0$时,若该题有两个正确选项,则小明从两个错误选项中
选择$1$个,从两个正确选项中选择$1$个,或选择两个错误选
项,若该题有三个正确选项,则小明选择错误选项,再从$3$
个正确选项中选择$1$个,所以$P(Y = 0)=\frac{1}{2} × \frac{C_{2}^{2}+C_{2}^{1}C_{2}^{1}}{C_{4}^{2}} × \frac{C_{2}^{1}C_{2}^{1}}{C_{3}^{1}}+$
$\frac{1}{2} × \frac{C_{3}^{1}C_{4}^{2}+C_{3}^{0}C_{4}^{3}}{C_{7}^{3}} × \frac{C_{3}^{1}}{C_{3}^{1}}=\frac{2}{3}$.因为$\frac{2}{3}>\frac{3}{8}$,所以$P(X = 0)<P(Y = 0)$,故$B$错误.
对于$C$,$X$的可能取值为$0,2,3$,其中$X = 2$,表示该题有$3$
个正确选项,小明从正确选项中选择$1$个,所以$P(X = 2)=\frac{1}{2}$
$× \frac{C_{3}^{1}}{C_{4}^{1}} × \frac{C_{3}^{1}}{C_{8}^{1}}=\frac{3}{8}$,所以$E(X)=0 × \frac{3}{8}+2 × \frac{3}{8}+3 × \frac{1}{4}=\frac{3}{2}$.$Y$的可能取
值为$0,4,6$,其中$Y = 6$,表示该题有$2$个正确选项,小明选择
了$2$个正确选项,所以$P(Y = 6)=\frac{1}{2} × \frac{C_{2}^{2}}{C_{4}^{2}}=\frac{1}{12}$,所以$E(Y)=$
$0 × \frac{2}{3}+4 × \frac{1}{4}+6 × \frac{1}{12}=\frac{3}{2}$.所以$E(X)=E(Y)$,故$C$正确.对
于$D$,$D(X)=(0 - \frac{3}{2})^{2} × \frac{3}{8}+\frac{1}{4} × (2 - \frac{3}{2})^{2}+\frac{3}{8} × (3 - \frac{3}{2})^{2} × \frac{1}{4}=$
$\frac{9}{4} × \frac{3}{8} × \frac{1}{4}+\frac{1}{4} × \frac{1}{4}+\frac{3}{8} × \frac{9}{4} × \frac{1}{4}=\frac{9}{4} × \frac{3}{8} × \frac{1}{2}+\frac{25}{4} × \frac{1}{4}+\frac{81}{4} × \frac{1}{12}=$
$\frac{19}{4}$,所以$D(X)<D(Y)$,故$D$正确.]
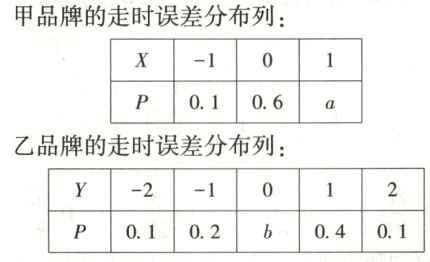
7. 【题型二、三】(2025·云南大学附中高二下月考)[ 多选 ] 某高中打算采购一批教室挂钟,现有甲、乙两种品牌的挂钟,已知甲、乙使用一年后它们的走时误差分别为 $ X $ 和 $ Y $(单位:秒),其分布列如下,则下列选项正确的是(
A.$ a = 0.3,b = 0.2 $
B.$ E(X) = E(Y) $
C.若 $ \eta = \frac{1}{2}X + 1 $,则 $ D(\eta) = 1.3 $
D.甲、乙两种品牌中甲的质量更稳定
ABD
)
A.$ a = 0.3,b = 0.2 $
B.$ E(X) = E(Y) $
C.若 $ \eta = \frac{1}{2}X + 1 $,则 $ D(\eta) = 1.3 $
D.甲、乙两种品牌中甲的质量更稳定
答案:
7.ABD[提示:对于$A$,由$0.1 + 0.6 + a = 1$,得$a = 1 - 0.1 - 0.6 =$
$0.3$,由$0.1 + 0.2 + b + 0.4 + 0.1 = 1$,得$b = 1 - 0.1 - 0.2 - 0.4 -$
$0.1 = 0.2$,故$A$正确;对于$B$,$E(X)=(-1) × 0.1+0 × 0.6 + 1 ×$
$0.3 = 0.2$,$E(Y)=(-2) × 0.1+(-1) × 0.2+0 × 0.3+1 × 0.4+$
$2 × 0.1 = 0.2$,所以$E(X)=E(Y)$,故$B$正确;对于$C$,$D(X)=$
$(-1 - 0.2)^{2} × 0.1+(0 - 0.2)^{2} × 0.6+(1 - 0.2)^{2} × 0.3 = 0.36$,因
为$\eta=\frac{1}{2}X + 1$,所以$D(\eta)=(\frac{1}{2})^{2}D(X)=\frac{1}{4} × 0.36 = 0.09$,
故$C$错误;对于$D$,$D(Y)=(-2 - 0.2)^{2} × 0.1+(-1 - 0.2)^{2} ×$
$0.2+(0 - 0.2)^{2} × 0.3+(1 - 0.2)^{2} × 0.4+(2 - 0.2)^{2} × 0.1 =$
$1.36$,因为$D(X)=0.36<D(Y)=1.36$,方差越小数据越稳
定,所以甲的质量更稳定,故$D$正确.]
$0.3$,由$0.1 + 0.2 + b + 0.4 + 0.1 = 1$,得$b = 1 - 0.1 - 0.2 - 0.4 -$
$0.1 = 0.2$,故$A$正确;对于$B$,$E(X)=(-1) × 0.1+0 × 0.6 + 1 ×$
$0.3 = 0.2$,$E(Y)=(-2) × 0.1+(-1) × 0.2+0 × 0.3+1 × 0.4+$
$2 × 0.1 = 0.2$,所以$E(X)=E(Y)$,故$B$正确;对于$C$,$D(X)=$
$(-1 - 0.2)^{2} × 0.1+(0 - 0.2)^{2} × 0.6+(1 - 0.2)^{2} × 0.3 = 0.36$,因
为$\eta=\frac{1}{2}X + 1$,所以$D(\eta)=(\frac{1}{2})^{2}D(X)=\frac{1}{4} × 0.36 = 0.09$,
故$C$错误;对于$D$,$D(Y)=(-2 - 0.2)^{2} × 0.1+(-1 - 0.2)^{2} ×$
$0.2+(0 - 0.2)^{2} × 0.3+(1 - 0.2)^{2} × 0.4+(2 - 0.2)^{2} × 0.1 =$
$1.36$,因为$D(X)=0.36<D(Y)=1.36$,方差越小数据越稳
定,所以甲的质量更稳定,故$D$正确.]
查看更多完整答案,请扫码查看


