《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

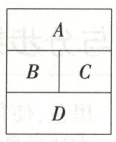
3. 【题型二】(原创题)哈尔滨冬奥会引发了全国冰雪运动的热潮,现某市准备在2025年冬季开展全市冰雪运动会,有来自四个阵营的观众队伍分别坐在$A,B,C,D$四个观众席位置(如图所示),为了区别现有4种不同颜色服装可以向他们提供,要求有公共边界的两个队伍不能用同一种颜色服装,则不同的方法种数为 (D)


A.24
B.28
C.36
D.48

答案： 3.D[提示：对于区域A，有4种颜色可选，对于区域B，与区域A相邻，有3种颜色可选，对于区域C，与区域A,B相邻，有2种颜色可选，对于区域D，与区域B,C相邻，有2种颜色可选，则不同的方法有4×3×2×2=48(种).]

4. 【题型三】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,三位同学按甲、乙、丙的顺序依次选一个作为礼物,如果让三位同学选取的礼物都满意,那么不同的选法有 (B)

A.360种
B.50种
C.60种
D.90种

答案： 4.B[提示：第一类：甲同学选择牛，乙有2种选法，丙有10种选法，则不同选法有1×2×10=20(种)；第二类：甲同学选择马，乙有3种选法，丙有10种选法，则不同选法有1×3×10=30(种).所以共有20+30=50种选法.]

5. 【题型三】[多选]已知数字0,1,2,3,4,由它们组成四位数,下列说法正确的有 (AB)

A.组成可以有重复数字的四位数有500个
B.组成无重复数字的四位数有96个
C.组成无重复数字的四位偶数有66个
D.组成百位是奇数的四位偶数有28个

答案： 5.AB[提示：对于A，组成可以有重复数字的四位数有4×5×5×5=500(个)，故A正确；对于B，组成无重复数字的四位数有4×4×3×2=96(个)，故B正确；对于C，若个位数为0，则有4×3×2=24(个)，若个位数不为0，则有2×3×3×2=36(个)，所以组成无重复数字的四位偶数有24+36=60(个)，故C错误；对于D，组成百位是奇数的四位偶数有4×2×5×3=120(个)，故D错误.]

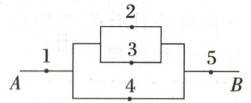
6. 【题型一、三】[多选]如图所示,线路从$A$到$B$之间有五个连接点,若连接点断开,可能导致线路不通,现发现$A,B$之间线路不通,则下列判断正确的是 (AC)


A.至多三个断点的有19种
B.至多三个断点的有22种
C.共有25种
D.共有28种

答案： 6.AC[提示：若有1个断点，则1,5中断开1个，有2种情况.若有2个断点，则1,5都断开有1种；1,5断开1个,2,3,4断开1个有2×3=6种，共1+6=7种情况.若有3个断点，则2,3,4断开有1种；1,5断开1个，2,3,4断开2个有2×3=6种，共1+3+6=10(种).若有4个断点，则1,5都断开，2,3,4断开2个有3种；1,5断开1个,2,3,4都断开有2种，共有3+2=5(种).若有5个断点，有1种情况.综上，至多三个断点的有2+7+10=19(种)，故A正确，B错误；所有情况共有2+7+10+5+1=25(种)，故C正确，D错误.]

7. 【题型三】(教材改编题)1800的不同的正奇数因数有9个.

答案： 7.9[提示：由题意得$1800=2^{3}×3^{2}×5^{2}，$所以1800的正因数$p=2^{r}×3^{s}×5^{t}(r,s,t∈N)，$由题意，r=0,1,2,t可取0,1,2.根据分步乘法计数原理可得不同的正奇数因数有1×3×3=9(个).]

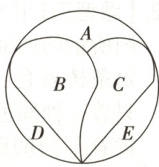
8. 【题型二】(2025·黑龙江大庆实验中学高二下期中)如图,积木拼盘由$A,B,C,D,E$五块积木组成,若每块积木都要涂一种颜色,且为了体现拼盘的特色,相邻的区域需涂不同的颜色(如:$A$与$B$为相邻区域,$A$与$D$为不相邻区域),现有五种不同的颜色可供挑选,则不同的涂色方法的种数是960.

答案： 8.960[提示：先涂A，则A有5种涂法，再涂B，因为B与A相邻，所以B的颜色只要与A不同即可，有4种涂法，同理C有3种涂法，D有4种涂法，E有4种涂法，由分步乘法计数原理可知，不同的涂色方法种数是5×4×3×4×4=960.]

9. 【题型一、二】某单位组织职工义务献血,在体检合格的人中,$O$型血的共有1人,$A$型血的共有16人,$B$型血的共有15人,$AB$型血的共有12人.
(1)从中任选1人去献血,有多少种不同的选法?
(2)从四种血型的人中各选1人去献血,有多少种不同的选法?

答案： 9.解：
(1)从O型血的人中选1人有1种不同的选法，从A型血的人中选1人有16种不同的选法，从B型血的人中选1人有15种不同的选法，从AB型血的人中选1人有12种不同的选法.任选1人去献血，由分类加法计数原理知，共有1+16+15+12=44种不同的选法.
(2)要从四种血型的人中各选1人，由分步乘法计数原理，共有1×16×15×12=2880种不同的选法.

用1,2,3,4四个数字(可重复)排成三位数,并把这些三位数由小到大排成一个数列$\{a_n\}$.
(1)这个数列共有多少项?
(2)若$a_n = 341$,求$n$的值.

答案： 解：
(1)由于每个数位上的数都有4种取法，由分步乘法计数原理，得满足条件的三位数有4×4×4=64(个).即这个数列共有64项.
(2)把比341小的数分为两类：第1类，百位上的数是1或2，十位和个位上的数分别可以是1,2,3,4中的任一个，这样的数的个数为2×4×4=32.第2类，百位上的数是3，十位上的数可以是1,2,3中的任一个，个位上的数可以是1,2,3,4中的任一个，这样的数的个数为3×4=12.所以比341小的数有32+12=44(个).所以n=44+1=45.
【易错点津】 注意
(1)中分步的标准是以三位数的数位为依据，分3步即可完成，答案是$4^{3}，$而不是$3^{4}.$