2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
4. 【题型二】(2025·陕西咸阳实验高二下月考) [多选] 一个袋子中有 3 个大小、质地相同的球,其中有 1 个红球、2 个白球,从袋中不放回摸球 2 次,每次摸 1 个球,记摸得红球个数为 $ X $;从袋中有放回摸球 2 次,每次摸 1 个球,记摸得红球个数为 $ Y $。则 (
A.$ X $ 的所有可能取值为 0 或 1
B.$ Y $ 的所有可能取值为 0 或 1
C.$ P(X = 1)=P(Y = 1) $
D.$ E(X)=E(Y) $
AD
)A.$ X $ 的所有可能取值为 0 或 1
B.$ Y $ 的所有可能取值为 0 或 1
C.$ P(X = 1)=P(Y = 1) $
D.$ E(X)=E(Y) $
答案:
4.AD[提示:对于A,由题意可得,摸得红球的个数为$0$或$1$,所以$X$的所有可能取值为$0$或$2$,故B错误;对于C,$P(X=1)=\frac{C_{1}^{1}}{C_{3}^{1}}=\frac{C_{1}^{1}}{C_{3}^{1}}=\frac{1}{3}$,
$P(Y=1)=\frac{C_{2}^{1}}{C_{3}^{1}}=\frac{2}{3}$,故C错误;对于D,$P(X=0)=\frac{C_{2}^{1}}{C_{3}^{1}}=\frac{1}{3},P(Y=0)=\frac{C_{2}^{1}}{C_{3}^{1}}=\frac{2}{3}$,$P(Y=2)=\frac{1}{3}$,所以$E(X)=0 × \frac{1}{3}+1 × \frac{2}{3}=\frac{2}{3}$,$E(Y)=0 × \frac{2}{9}+1 × \frac{4}{9}+2 × \frac{2}{3}=\frac{2}{3}$,所以$E(X)=E(Y)$,故D正确.]
$P(Y=1)=\frac{C_{2}^{1}}{C_{3}^{1}}=\frac{2}{3}$,故C错误;对于D,$P(X=0)=\frac{C_{2}^{1}}{C_{3}^{1}}=\frac{1}{3},P(Y=0)=\frac{C_{2}^{1}}{C_{3}^{1}}=\frac{2}{3}$,$P(Y=2)=\frac{1}{3}$,所以$E(X)=0 × \frac{1}{3}+1 × \frac{2}{3}=\frac{2}{3}$,$E(Y)=0 × \frac{2}{9}+1 × \frac{4}{9}+2 × \frac{2}{3}=\frac{2}{3}$,所以$E(X)=E(Y)$,故D正确.]
5. 【题型二】小林从 $ A $ 地出发去往 $ B $ 地,1 小时内到达的概率为 0.4,1 小时 10 分到达的概率为 0.3,1 小时 20 分到达的概率为 0.3。现规定 1 小时内到达的奖励为 200 元,若超过 1 小时到达,则每超过 1 分钟奖励少 2 元。设小林最后获得的奖励为 $ X $ 元,则 $ E(X) $ 等于 (
A.176
B.182
C.184
D.186
B
)A.176
B.182
C.184
D.186
答案:
5.B[提示:依题意可得$X$的可能取值为$200,180,160,P(X=200)=0.4,P(X=180)=0.3,P(X=160)=0.3$,则$X$的分布列为: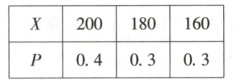
所以$E(X)=200 × 0.4+(180+160) × 0.3=182.$]
5.B[提示:依题意可得$X$的可能取值为$200,180,160,P(X=200)=0.4,P(X=180)=0.3,P(X=160)=0.3$,则$X$的分布列为:

所以$E(X)=200 × 0.4+(180+160) × 0.3=182.$]
6. 【题型二】小芳用人体语言把成语的意思传递给本组其他同学。若小组内同学甲猜对成语的概率是 0.4,同学乙猜对成语的概率是 0.5,且规定猜对得 1 分,猜不对得 0 分,则这两个同学各猜 1 次,得分之和 $ X $(单位:分)的均值为 (
A.0.9
B.0.8
C.1.2
D.1.1
A
)A.0.9
B.0.8
C.1.2
D.1.1
答案:
6.A[提示:由题意可知随机变量$X$的可能取值有$0,1,2,P(X=0)=0.6 × 0.5=0.3,P(X=1)=0.4 × 0.5+0.6 × 0.5=0.5,P(X=2)=0.4 × 0.5=0.2$,因此$E(X)=0 × 0.3+1 × 0.5+2 × 0.2=0.9.$]
7. 【题型二、三】在一次社团活动中,甲、乙两人进行象棋比赛,规定每局比赛获胜的一方得 3 分,负的一方得 1 分(假设没有平局)。已知甲胜乙的概率为 0.6,若甲、乙两人比赛两局,且两局比赛结果互不影响。设两局比赛结束后甲的得分为 $ \xi $,则 $ E(\xi)=$
4.4
$$ _ 。
答案:
7.4.4[提示:$\xi$可能的取值分别为$2,4,6,P(\xi=2)=0.4 × 0.4=0.16,P(\xi=4)=C_{2}^{1} × 0.6 × 0.4=0.48,P(\xi=6)=0.6 × 0.6=0.36$,所以$E(\xi)=2 × 0.16+4 × 0.48+6 × 0.36=4.4.$]
8. 【题型二】已知盒中装有 $ n(n>1) $ 个红球和 3 个黄球,从中任取 2 个球(取到每个球是等可能的),随机变量 $ X $ 表示取到黄球的个数,且 $ X $ 的分布列如下表,则 $ E(X)=$
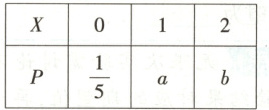
1
_ 。
答案:
8.1[提示:由题意知$P(X=0)=\frac{C_{n+3}^{2}}{C_{n+3}^{2}}=\frac{1}{5}$,解得$n=3$或$n=-\frac{1}{2}$(舍去).由$n=3$知$a=P(X=1)=\frac{C_{3}^{1}C_{3}^{2}}{C_{6}^{3}}=\frac{3}{5},b=P(X=2)=\frac{C_{3}^{2}}{C_{6}^{3}}=\frac{1}{5}$,所以$E(X)=0 × \frac{1}{5}+1 × \frac{3}{5}+2 × \frac{1}{5}=1.$]
9. 【题型三】甲、乙两工人在一天生产中出现的废品数分别是两个随机变量 $ X,Y $,其分布列分别为:
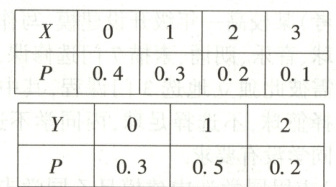
若甲、乙两人的日产量相等,则甲、乙两人中技术较好的是

若甲、乙两人的日产量相等,则甲、乙两人中技术较好的是
乙
_ 。
答案:
9.乙[提示:由题意,$E(X)=0 × 0.4+1 × 0.3+2 × 0.2+3 × 0.1=1$,$E(Y)=0 × 0.3+1 × 0.5+2 × 0.2=0.9,\because E(Y)<E(X),\therefore$乙技术较好.]
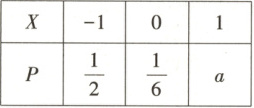
10. 【题型一】(2025·黑龙江牡丹江一中高二下期中) 已知 $ X $ 的分布列如下表,设 $ Y = 2X + 1 $,则 $ Y $ 的数学期望 $ E(Y) $ 的值是
$\frac{2}{3}$
_ 。
答案:
10.$\frac{2}{3}$[提示:由已知得$\frac{2}{3}+\frac{1}{6}+a=1,\therefore a=\frac{1}{3},\therefore E(X)=2E(X)+1,E(Y)=\frac{1}{2} × \frac{1}{3}=-\frac{1}{6},\therefore E(X)=2 × (-\frac{1}{6})+1=\frac{2}{3}.$]
11. 【题型二、三】(2025·吉林长春十一高中高二下月考) 甲、乙两人共同参加某公司的面试,面试分为初试和复试,若初试不通过,则不用参加复试,复试通过则被录用,否则不被录用。已知甲通过初试和复试的概率分别为 $ \frac{2}{3},\frac{1}{3} $,乙通过初试和复试的概率均为 $ \frac{1}{2} $,两人是否通过面试相互独立。
(1) 求甲、乙两人中至少有 1 人通过初试且没有通过复试的概率;
(2) 设两人中被录用的人数为 $ X $,求 $ X $ 的分布列及数学期望。
(1) 求甲、乙两人中至少有 1 人通过初试且没有通过复试的概率;
(2) 设两人中被录用的人数为 $ X $,求 $ X $ 的分布列及数学期望。
答案:
11.解:
(1)记“甲、乙两人中至少有$1$人通过初试且没有通过复试”为事件$A$,甲通过初试且没有通过复试的概率为$P_{1}=\frac{2}{3} × (1-\frac{1}{3})=\frac{4}{9}$,乙通过初试且没有通过复试的概率为$P_{2}=\frac{1}{2} × (1-\frac{1}{2})=\frac{1}{4}$,所以$P(A)=1-(1-P_{1})(1-P_{2})=1-(1-\frac{4}{9}) × (1-\frac{1}{4})=\frac{7}{12}$,即甲、乙两人中至少有$1$人通过初试且没有通过复试的概率为$\frac{7}{12}$.
(2)由题意知$X$的所有可能取值为$0,1,2$.甲被录用的概率为$\frac{2}{3} × \frac{1}{3}=\frac{2}{9}$,乙被录用的概率为$\frac{1}{2} × \frac{1}{2}=\frac{1}{4}$,所以$P(X=0)=(1-\frac{2}{9}) × (1-\frac{1}{4})=\frac{7}{12},P(X=1)=(1-\frac{2}{9}) × \frac{1}{4}+\frac{2}{9} × (1-\frac{1}{4})=\frac{13}{36}$,$P(X=2)=\frac{2}{9} × \frac{1}{4}=\frac{1}{18}$,所以$X$的分布列为: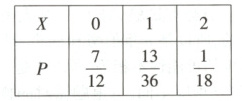
故$E(X)=0 × \frac{7}{12}+1 × \frac{13}{36}+2 × \frac{1}{18}=\frac{17}{36}$.
11.解:
(1)记“甲、乙两人中至少有$1$人通过初试且没有通过复试”为事件$A$,甲通过初试且没有通过复试的概率为$P_{1}=\frac{2}{3} × (1-\frac{1}{3})=\frac{4}{9}$,乙通过初试且没有通过复试的概率为$P_{2}=\frac{1}{2} × (1-\frac{1}{2})=\frac{1}{4}$,所以$P(A)=1-(1-P_{1})(1-P_{2})=1-(1-\frac{4}{9}) × (1-\frac{1}{4})=\frac{7}{12}$,即甲、乙两人中至少有$1$人通过初试且没有通过复试的概率为$\frac{7}{12}$.
(2)由题意知$X$的所有可能取值为$0,1,2$.甲被录用的概率为$\frac{2}{3} × \frac{1}{3}=\frac{2}{9}$,乙被录用的概率为$\frac{1}{2} × \frac{1}{2}=\frac{1}{4}$,所以$P(X=0)=(1-\frac{2}{9}) × (1-\frac{1}{4})=\frac{7}{12},P(X=1)=(1-\frac{2}{9}) × \frac{1}{4}+\frac{2}{9} × (1-\frac{1}{4})=\frac{13}{36}$,$P(X=2)=\frac{2}{9} × \frac{1}{4}=\frac{1}{18}$,所以$X$的分布列为:

故$E(X)=0 × \frac{7}{12}+1 × \frac{13}{36}+2 × \frac{1}{18}=\frac{17}{36}$.
查看更多完整答案,请扫码查看


