《2025年零失误分层训练高二数学选择性必修第三册黑吉辽内蒙古专版》

1. 一箱中装有 6 个同样大小的红球，编号分别为 1，2，3，4，5，6，还有 4 个同样大小的黄球，编号分别为 7，8，9，10。现从箱中任取 4 个球，下列变量服从超几何分布的是(C)

A.$X$ 表示取出的最小号码
B.若有放回地取球时，$X$ 表示取出的最大号码
C.$X$ 表示取出的红球个数
D.若有放回地取球时，$X$ 表示取出的黄球个数

答案： 1.C[提示：对于A,B,D，不符合超几何分布的定义，因为超几何分布取球必须是无放回取球，所以A,B,D错误；对于C，将红球个数视为次品数，黄球个数视为正品数，则可以用超几何分布的数学模型计算概率.]

2. 下列随机变量中，服从超几何分布的有①②。(填序号)
①在 10 件产品中有 3 件次品，一件一件地不放回地任意取出 4 件，记取到的次品数为 $X$；②从 3 名男同学和 2 名女同学中任意抽取 2 名学生，记 $X$ 表示所取的 2 名学生中男同学的人数；③一名学生骑自行车上学，途中有 6 个交通岗，记此学生遇到红灯数为随机变量 $X$。

答案： 2.①②[提示：根据超几何分布的定义可知，①中随机变量$X$服从超几何分布，②中随机变量$X$也服从超几何分布，而③显然不能看作一个不放回抽样问题，故随机变量$X$不服从超几何分布.]

3. 从 3 台甲型彩电和 2 台乙型彩电中任取 2 台，若设 $X$ 表示所取的 2 台彩电中甲型彩电的台数，则 $P(X = 1)=$$\frac{3}{5}$。

答案： 3.$\frac{3}{5}$[提示：可利用超几何分布概率模型的知识求解.$X = 1$表示的结果是抽取的2台彩电中有甲型和乙型彩电各一台，故所求概率$P(X = 1) = \frac{C_{3}^{1}C_{2}^{1}}{C_{5}^{2}} = \frac{3}{5}$.]

4. 在某次国际会议中，需要从 4 个中国人、5 个英国人和 6 个美国人中任选 4 人负责新闻发布会，则恰好选中 3 个英国人的概率为$\frac{C_{5}^{3}C_{10}^{1}}{C_{15}^{4}}$。(用式子表示)

答案： 4.$\frac{C_{5}^{3}C_{10}^{1}}{C_{15}^{4}}$[提示：设选取的4人中英国人有$X$个，由题意知$X$服从参数为$N = 15,M = 5,n = 4$的超几何分布，其中$X$的可能取值为0,1,2,3,4，且$P(X = k) = \frac{C_{5}^{k} · C_{10}^{4 - k}}{C_{15}^{4}}(k = 0,1,2,3,4)$.
所以$P(X = 3) = \frac{C_{5}^{3}C_{10}^{1}}{C_{15}^{4}}$.]

5.（教材改编题）学校要从 12 名候选人中选 4 名同学组成学生会，已知有 4 名候选人来自甲班，假设每名候选人都有相同的机会被选到。
（1）求恰有 1 名甲班的候选人被选中的概率；
（2）用 $X$ 表示选中的候选人中来自甲班的人数，求 $P(X\geq3)$。

答案： 5.解：
(1)记事件$A$为恰有1名甲班的候选人被选中，则$P(A)$
$ = \frac{C_{4}^{1}C_{8}^{3}}{C_{12}^{4}} = \frac{224}{495}$.
(2)$P(X \geq 3) = P(X = 3) + P(X = 4) = \frac{C_{4}^{3}C_{8}^{1}}{C_{12}^{4}} +$
$\frac{C_{4}^{4}}{C_{12}^{4}} = \frac{1}{15}$.

6. 有 $N$ 件产品，其中有 $M$ 件次品，从中不放回地抽 $n$ 件产品，抽到的正品数的数学期望值是(B)

A.$n·\frac{M}{N}$
B.$n·\frac{N - M}{N}$
C.$(n - 1)·\frac{M}{N}$
D.$(n - 1)·\frac{N - M}{N}$

答案： 6.B[提示：由题意，有$N$件产品，其中有$M$件次品，从中不放回地抽$n$件产品，则抽到正品数$X$服从超几何分布，所以抽到的正品数的数学期望值是$E(X) = n · \frac{N - M}{N}$.]

7.(教材改编题)某品牌饮料正在进行有奖促销活动，一盒 5 瓶装的饮料中有 2 瓶有奖，消费者从中随机取出 2 瓶，记 $X$ 为其中有奖的瓶数，则 $E(X)$ 等于(C)

A.$\frac{2}{5}$
B.$\frac{3}{5}$
C.$\frac{4}{5}$
D.1

答案： 7.C[提示：依题意，$X$的可能取值为0,1,2，所以$P(X = 0) =$
$\frac{C_{5}^{2}}{C_{5}^{2}} = \frac{3}{10}$,$P(X = 1) = \frac{C_{3}^{1}C_{2}^{1}}{C_{5}^{2}} = \frac{3}{5}$,$P(X = 2) = \frac{C_{2}^{2}}{C_{5}^{2}} = \frac{1}{10}$,故$E(X) = 0 ×$
$\frac{3}{10} + 1 × \frac{3}{5} + 2 × \frac{1}{10} = \frac{4}{5}$.]

8. 一个袋中装有大小相同的 8 个小球，其中有 5 个红球、3 个黑球，现从中随机摸出 3 个球。
（1）求至少摸到 1 个红球的概率；
（2）求摸到红球的个数 $\xi$ 的分布列及数学期望。

答案： 8.解：
(1)设至少摸到1个红球为事件$A$，则$P(A) = 1 - \frac{C_{3}^{3}}{C_{8}^{3}} =$
$\frac{55}{56}$.
(2)$\xi$服从超几何分布，$P(\xi = k) = \frac{C_{5}^{k} · C_{3}^{3 - k}}{C_{8}^{3}}(k = 0,1,$
2,3),$P(\xi = 0) = \frac{C_{5}^{0} · C_{3}^{3}}{C_{8}^{3}} = \frac{1}{56}$,$P(\xi = 1) = \frac{C_{5}^{1} · C_{3}^{2}}{C_{8}^{3}} = \frac{15}{56}$,$P(\xi =$
$2) = \frac{C_{5}^{2} · C_{3}^{1}}{C_{8}^{3}} = \frac{30}{56} = \frac{15}{28}$,$P(\xi = 3) = \frac{C_{5}^{3} · C_{3}^{0}}{C_{8}^{3}} = \frac{10}{56} = \frac{5}{28}$.所以摸到红球的个数$\xi$的分布列为：
$\xi$ 0 1 2 3
$P$ $\frac{1}{56}$ $\frac{15}{56}$ $\frac{15}{28}$ $\frac{5}{28}$
$E(\xi) = 0 × \frac{1}{56} + 1 × \frac{15}{56} + 2 × \frac{15}{28} + 3 × \frac{5}{28} = \frac{15}{8}$.

9. 某学校在寒假期间安排了“垃圾分类知识普及及实践活动”。为了解学生的学习成果，该校从全校学生中随机抽取了 50 名学生作为样本进行测试，记录他们的成绩，测试卷满分 100 分，将数据分成 6 组：$[40,50)$，$[50,60)$，$[60,70)$，$[70,80)$，$[80,90)$，$[90,100]$，并整理得到如图所示的频率分布直方图。

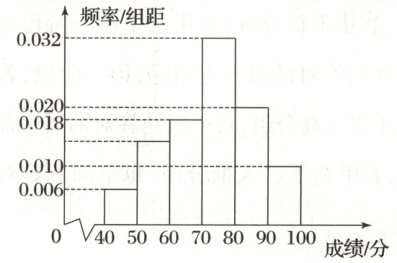
（1）若全校学生参加同样的测试，试估计全校学生的平均成绩（每组成绩用中间值代替）；
（2）在样本中，从其成绩在 80 分及以上的学生中随机抽取 3 人，用 $X$ 表示其成绩在 $[90,100]$ 中的人数，求 $X$ 的分布列及数学期望；
（3）在（2）抽取的 3 人中，用 $Y$ 表示其成绩在 $[80,90)$ 的人数，试判断方差 $D(X)$ 与 $D(Y)$ 的大小。（直接写出结果）

答案： 9.解：
(1)由频率分布直方图可得第二组的频率为$1 - 0.06 -$
$0.18 - 0.32 - 0.20 - 0.10 = 0.14$，$\therefore$全校学生的平均成绩为
$45 × 0.06 + 55 × 0.14 + 65 × 0.18 + 75 × 0.32 + 85 × 0.20 + 95 × 0.10$
$= 72.6$(分).
(2)由题可知成绩在80分及以上的学生共有$50 × (0.20 + 0.10) = 15$(人)，其中$[90,100]$中有5人，所以$X$可取0,1,2,3，则$P(X = 0) = \frac{C_{10}^{0}C_{5}^{3}}{C_{15}^{3}} = \frac{24}{91}$，$P(X = 1) = \frac{C_{10}^{1}C_{5}^{2}}{C_{15}^{3}} = \frac{45}{91}$，$P(X = 2) =$
$\frac{C_{10}^{2}C_{5}^{1}}{C_{15}^{3}} = \frac{20}{91}$，$P(X = 3) = \frac{C_{10}^{3}C_{5}^{0}}{C_{15}^{3}} = \frac{2}{91}$，所以$X$的分布列为：
$X$ 0 1 2 3
$P$ $\frac{24}{91}$ $\frac{45}{91}$ $\frac{20}{91}$ $\frac{2}{91}$
故$E(X) = 0 × \frac{24}{91} + 1 × \frac{45}{91} + 2 × \frac{20}{91} + 3 × \frac{2}{91} = 1$.
(3)$D(X) = D(Y)$.