《2025年全品学练考七年级数学上册华师大版》

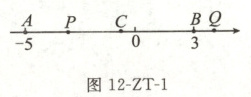
1. 如图 12-ZT-1，已知数轴上的 $ A $，$ B $ 两点对应的数分别为 $ -5 $，$ 3 $，点 $ P $，$ Q $ 同时分别从点 $ A $，$ B $ 出发沿数轴正方向运动，点 $ P $ 的运动速度为 $ m $ 个单位长度/秒，点 $ Q $ 的运动速度为 $ n $ 个单位长度/秒，在运动过程中，取线段 $ AQ $ 的中点 $ C $(点 $ C $ 始终在线段 $ PQ $ 上)，若线段 $ PC $ 的长度总为一个固定的值，则 $ m $ 与 $ n $ 应满足的数量关系是$n=2m$。

答案： 1. $n=2m$

2. 如图 12-ZT-2，$ B $ 是线段 $ AD $ 上的一个动点，沿 $ A \to D \to A $ 以 $ 2 $ cm/s 的速度往返运动 $ 1 $ 次，$ C $ 是线段 $ BD $ 的中点，$ AD = 10 $ cm，设点 $ B $ 运动的时间为 $ t $ s($ t $ 不超过 $ 10 $)。
(1)当 $ t = 2 $ 时，$ AB = $4 cm。
(2)当 $ t = 8 $ 时，求线段 $ CD $ 的长。
(3)在运动过程中，若 $ AB $ 的中点为 $ E $，则 $ CE $ 的长是否变化？若不变，求出 $ CE $ 的长；若发生变化，请说明理由。

答案： 2.
(1)4
(2)$3 cm$
(3)CE的长不变，为$5 cm$

3. 已知 $ \angle AOB = 50° $，$ OC $ 是可绕点 $ O $ 旋转的射线，当 $ \angle BOC = 32° $ 时，$ \angle AOC $ 的度数是(C)

A.$ 18° $
B.$ 82° $
C.$ 18° $ 或 $ 82° $
D.$ 82° $ 或 $ 50° $

答案： 3. C

4. 如图 12-ZT-3，已知 $ O $ 是直线 $ AB $ 上的一点，$ \angle COD $ 是直角，$ OE $ 平分 $ \angle BOC $。
（1）①若 $ \angle AOC = 60° $，求 $ \angle DOE $ 的度数；
②若 $ \angle AOC = \alpha $，直接写出 $ \angle DOE $ 的度数（用含 $ \alpha $ 的式子表示）。
（2）将图（a）中的 $ \angle DOC $ 绕点 $ O $ 顺时针旋转至图（b）所示的位置，试探究 $ \angle DOE $ 和 $ \angle AOC $ 之间的数量关系，写出你的结论，并说明理由。

答案： 4. 解：
(1)①因为$\angle AOC = 60°$，所以$\angle BOC = 180° - \angle AOC = 180° - 60° = 120°$。
因为OE平分$\angle BOC$，所以$\angle COE = \frac{1}{2} \angle BOC = \frac{1}{2} × 120° = 60°$。
又因为$\angle COD = 90°$，所以$\angle DOE = \angle COD - \angle COE = 90° - 60° = 30°$。
②因为$\angle COD$是直角，$\angle AOC = \alpha$，
所以$\angle COB = 180° - \alpha$。
因为OE平分$\angle BOC$，
所以$\angle COE = \frac{1}{2} \angle BOC = 90° - \frac{1}{2} \alpha$，
所以$\angle DOE = \angle COD - \angle COE = 90° - \left(90° - \frac{1}{2} \alpha\right) = \frac{1}{2} \alpha$。
(2)$\angle DOE = \frac{1}{2} \angle AOC$。理由如下：
因为$\angle BOC = 180° - \angle AOC$，OE平分$\angle BOC$，所以$\angle COE = \frac{1}{2} \angle BOC = \frac{1}{2} (180° - \angle AOC) = 90° - \frac{1}{2} \angle AOC$。
所以$\angle DOE = \angle COD - \angle COE = 90° - \left(90° - \frac{1}{2} \angle AOC\right) = \frac{1}{2} \angle AOC$。