《2025年全品学练考七年级数学上册华师大版》

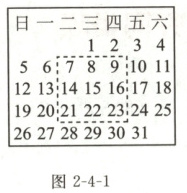
10. 图 2-4-1 是某月的月历，现用一长方形在月历中任意框出 9 个数 $ \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} $，用含 $ e $ 的代数式表示出这 9 个数的和为9e.

答案： 10. 9e

11. 阅读材料：计算 $ (-3x^{3} + 5x^{2} - 7) + (2x - 3 + 3x^{2}) $ 时，可列竖式：
$\begin{array}{r}-3x^{3} + 5x^{2} \quad -7 \\+ \quad 3x^{2} + 2x - 3 \\\hline-3x^{3} + 8x^{2} + 2x - 10\end{array}$
小明认为，整式的加减实际上就是合并同类项，而合并同类项的关键是合并各同类项的系数，因此，可把上面的竖式简化为：
$\begin{array}{r}-3 + 5 + 0 - 7 \\+ \quad 0 + 3 + 2 - 3 \\\hline-3 + 8 + 2 - 10\end{array}$
所以原式 $ = -3x^{3} + 8x^{2} + 2x - 10 $.
根据材料解答下列问题：
已知 $ A = -2x - 3x^{3} + 1 + x^{4} $，$ B = 2x^{3} - 4x^{2} + x $.
(1) 将 $ A $ 按 $ x $ 的降幂排列：x⁴-3x³-2x+1.
(2) 请仿照小明的方法计算 $ A - B $.

答案： 11.
(1)x⁴-3x³-2x+1
(2)列竖式为：1 -3+0 -2+1 0+2 -4+1+0 1 -5+4 -3+1 所以原式=x⁴-5x³+4x²-3x+1.

12. 已知单项式 $ x^{3}y^{m + 1} $ 与单项式 $ \frac{1}{2}x^{n - 1}y^{2} $ 的和也是单项式.
(1) 求 $ m $，$ n $ 的值；
(2) 当 $ x = 1 $，$ y = 2 $ 时，求 $ x^{3}y^{m + 1} + \frac{1}{2}x^{n - 1}y^{2} $ 的值.

答案： 12.
(1)m=1 n=4
(2)6

1. 若关于 $ x $ 的多项式 $ 3x^{3} + k^{2}x^{2} - 4x^{2} + x - 5 $ 合并同类项后不含 $ x^{2} $ 项，则 $ k $ 的值为(D)

A.0
B.2
C.-2
D.2 或 -2

答案： 1. D

2. 关于 $ x $，$ y $ 的代数式 $ axy - 3x^{2} + 2xy + bx^{2} + y $ 合并同类项后不含二次项，则 $ (a + b)^{2025} = $1.

答案： 2. 1

3. 新考法探究性 请回答下列问题：
(1) 若关于 $ x $，$ y $ 的多项式 $ mx^{2} + 3xy - 2y^{2} - x^{2} + nxy - 2y + 6 $ 的值与 $ x $ 的取值无关，求 $ (m + n)^{3} $ 的值；
(2) 若关于 $ x $，$ y $ 的多项式 $ 6mx^{2} + 4nxy + 2x + 2xy - x^{2} + y + 4 $ 合并同类项后不含二次项，求 $ m - n $ 的值.

答案： 3.
(1)-8
(2)2/3