《2025年全品学练考七年级数学上册华师大版》

10. 图 3 - 3 - 12 是一个正方体，则它的表面展开图可能是图 3 - 3 - 13 中的(A)

答案： 10. A

11. 如图 3 - 3 - 14 是一个无盖正方体盒子，盒底标有一个字母 $m$，现沿箭头所指方向将盒子剪开，则展开后的图形是(A)

答案： 11. A

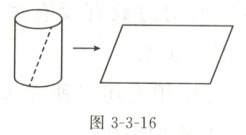
12. 一个半径为 $3 cm$，高为 $5 cm$ 的圆柱，将它的侧面沿虚线剪开(如图 3 - 3 - 16)，剪开后得到一个平行四边形，这个平行四边形的面积是30π cm²。

答案： 12. $30\pi\ cm^{2}$

13. 图 3 - 3 - 17 是一个多面体的表面展开图，每个面上都标注了字母（所有字母都写在这一多面体的外表面），请根据要求回答问题：
（1）如果面 $F$ 在前面，从左面看是面 $B$，那么哪一面会在上面？
（2）如果从右面看是面 $C$，面 $D$ 在后面，那么哪一面会在上面？
（3）如果面 $A$ 在多面体的底部，从右面看是面 $B$，那么哪一面会在前面？

答案： 13. 解：
(1)面 C.
(2)面 A.
(3)面 C.

14. 数学思想 数形结合 如图 3 - 3 - 18 所示的是一个无盖正方体纸盒的表面展开图，请解答下列问题：
(1)若在图中补上一个同样大小的正方形 $F$，使其成为一个正方体的表面展开图，共有4种补法；
(2)请画出(1)中的其中一种补法；
(3)设 $A = a^{3}+a^{2}b + 3$，$B = a^{2}b - 3$，$C = a^{3}-1$，$D = 6 - a^{2}b$，若(2)中的展开图围成正方体后，相对两个面上的代数式之和都相等，分别求 $E$，$F$ 所代表的代数式。

答案：
14. 解：
(1)4
(2)如图所示(画出其中一种即可).

(3)根据题意，得 A所在面与 D所在面是相对面，
C所在面与 E所在面是相对面，
B所在面与 F所在面是相对面.
$A + D = a^{3}+a^{2}b + 3 + 6 - a^{2}b = a^{3}+ 9$，
所以$E = a^{3}+ 9 - (a^{3}- 1)=10$，
$F = a^{3}+ 9 - (a^{2}b - 3)=a^{3}-a^{2}b + 12$.