《2025年全品学练考七年级数学上册华师大版》

1. 化简$-(m-n)$的结果是(D)

A.$m-n$
B.$m+n$
C.$-m-n$
D.$-m+n$

答案： 1. D

2. 下列各式中，去括号化简得$3a-2b+c$的是(D)

A.$3a-(2b+c)$
B.$c-(2b+3a)$
C.$-(-3a-2b)+c$
D.$3a-(2b-c)$

答案： 2. D

3. 下列去括号正确的是(D)

A.$a+(-2b+c)=a+2b+c$
B.$a-2(-2b+c)=a+4b-c$
C.$a-2(-2b+c)=a+4b+2c$
D.$a-(-2b+c)=a+2b-c$

答案： 3. D

4. (1)去括号：$-x+2(y-2)=$-x + 2y - 4；
(2)去括号：$2a-3(b+c-d)=$2a - 3b - 3c + 3d；
(3)化简：$2xy-(3xy-3y^{2}+5)=$-xy + 3y² - 5.

答案： 4.
(1)$-x + 2y - 4$
(2)$2a - 3b - 3c + 3d$
(3)$-xy + 3y^{2} - 5$

5. 去括号并按$x$的升幂排列：$9-3(x^{2}-2x+x^{3})=$9 + 6x - 3x² - 3x³.

答案： 5. $9 + 6x - 3x^{2} - 3x^{3}$

6. 化简$a-[-2a-(a-b)]$的结果是(B)

A.$2a-b$
B.$4a-b$
C.$-2a$
D.$2a-2b$

答案： 6. B

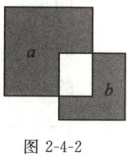
7. 如图2-4-2，两个正方形的面积分别为16，9，两个阴影图形的面积分别为$a$，$b$，则$a-b=$7.

答案： 7. 7

8. 多项式$mx^{2}-(1-x-6x^{2})$化简后不含$x$的二次项，则$m$的值为-6.

答案： 8. $-6$

9. 先去括号，再合并同类项：
(1)$x-2(x+1)+3x$；
(2)$3(5m-6n)+2(3m-4n)$；
(3)$4a^{2}+2(3ab-2a^{2})-(7ab-1)$；
(4)$3(2x^{2}-y^{2})-2(3y^{2}-2x^{2})$.

答案： 9. 解：
(1)$x - 2(x + 1) + 3x$
$= x - 2x - 2 + 3x$
$= 2x - 2$.
(2)$3(5m - 6n) + 2(3m - 4n)$
$= 15m - 18n + 6m - 8n$
$= 21m - 26n$.
(3)$4a^{2} + 2(3ab - 2a^{2}) - (7ab - 1)$
$= 4a^{2} + 6ab - 4a^{2} - 7ab + 1$
$= -ab + 1$.
(4)$3(2x^{2} - y^{2}) - 2(3y^{2} - 2x^{2})$
$= 6x^{2} - 3y^{2} - 6y^{2} + 4x^{2}$
$= 10x^{2} - 9y^{2}$.

10. 数学思想 数形结合 已知$a$，$b$，$c$在数轴上的对应点的位置如图2-4-3所示
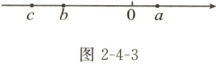
(1)用“$＞$”“$＜$”填空：
$a+b$＜$0$，$c-a$＜$0$，$b+c$＜$0$；
(2)化简：$|a|-|a+b|+|c-a|+|b+c|$.

答案： 10. 解：
(1)$＜ ＜ ＜$
(2)原式$= a - (-a - b) + (a - c) + (-b - c) = a + a + b + a - c - b - c = 3a - 2c$.