第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
11. 下列说法不正确的是(
A.若点 $ C $ 在线段 $ BA $ 的延长线上,则 $ BA = AC - BC $
B.若点 $ C $ 在线段 $ AB $ 上,则 $ AB = AC + BC $
C.若 $ AC + BC > AB $,则点 $ C $ 一定在线段 $ AB $ 外
D.若 $ A $,$ B $,$ C $ 三点不在一条直线上,则 $ AB < AC + BC $
A
)A.若点 $ C $ 在线段 $ BA $ 的延长线上,则 $ BA = AC - BC $
B.若点 $ C $ 在线段 $ AB $ 上,则 $ AB = AC + BC $
C.若 $ AC + BC > AB $,则点 $ C $ 一定在线段 $ AB $ 外
D.若 $ A $,$ B $,$ C $ 三点不在一条直线上,则 $ AB < AC + BC $
答案:
11. A
12. $ A $,$ B $,$ C $ 三点在同一条直线上,$ M $,$ N $ 分别为 $ AB $,$ BC $ 的中点,且 $ AB = 60 $,$ BC = 40 $,则 $ MN $ 的长为(
A.$ 30 $
B.$ 30 $ 或 $ 10 $
C.$ 50 $
D.$ 50 $ 或 $ 10 $
D
)A.$ 30 $
B.$ 30 $ 或 $ 10 $
C.$ 50 $
D.$ 50 $ 或 $ 10 $
答案:
12. D
13. 已知线段 $ AB $,延长线段 $ AB $ 到点 $ C $,使 $ BC = \frac{1}{3}AB $,$ D $ 为 $ AC $ 的中点,若 $ AB = 9\ cm $,则 $ DC $ 的长为
6cm
。
答案:
13. 6cm
14. 如图 3 - 5 - 17,$ D $ 是线段 $ AC $ 的中点,$ B $ 是线段 $ AD $ 上一点,且 $ AB = \frac{3}{4}BC $。
(1) 若 $ BC = 8 $,求 $ CD $ 的长;
(2) 若 $ E $ 是 $ BC $ 的中点,$ CE = 12 $,求 $ AE $ 的长。
]

(1) 若 $ BC = 8 $,求 $ CD $ 的长;
(2) 若 $ E $ 是 $ BC $ 的中点,$ CE = 12 $,求 $ AE $ 的长。
]

答案:
14.
(1)7
(2)30
(1)7
(2)30
15. 如图 3 - 5 - 18,已知线段 $ AB $,延长线段 $ BA $ 至点 $ C $,使 $ CB = \frac{4}{3}AB $。
(1) 请根据题意将图形补充完整,直接写出 $ \frac{AC}{AB} = $
(2) 设 $ AB = 9\ cm $,点 $ D $ 从点 $ B $ 出发,点 $ E $ 从点 $ A $ 出发,分别以 $ 3\ cm/s $,$ 1\ cm/s $ 的速度沿直线 $ AB $ 向左运动。设运动时间为 $ t\ s $。
① 当点 $ D $ 在线段 $ AB $ 上运动时,求 $ \frac{AD}{CE} $ 的值;
② 在点 $ D $,$ E $ 沿直线 $ AB $ 向左运动的过程中,$ M $,$ N $ 分别是线段 $ DE $,$ AB $ 的中点。当 $ C $ 恰好为线段 $ BD $ 的三等分点时,求 $ MN $ 的长。
]
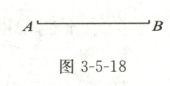
(1) 请根据题意将图形补充完整,直接写出 $ \frac{AC}{AB} = $
$\frac{1}{3}$
。(2) 设 $ AB = 9\ cm $,点 $ D $ 从点 $ B $ 出发,点 $ E $ 从点 $ A $ 出发,分别以 $ 3\ cm/s $,$ 1\ cm/s $ 的速度沿直线 $ AB $ 向左运动。设运动时间为 $ t\ s $。
① 当点 $ D $ 在线段 $ AB $ 上运动时,求 $ \frac{AD}{CE} $ 的值;
② 在点 $ D $,$ E $ 沿直线 $ AB $ 向左运动的过程中,$ M $,$ N $ 分别是线段 $ DE $,$ AB $ 的中点。当 $ C $ 恰好为线段 $ BD $ 的三等分点时,求 $ MN $ 的长。
]

答案:
15. 解:
(1)补充完整图形如图.
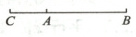
因为CB=$\frac{4}{3}AB$,
所以AC=$\frac{1}{3}AB$,
所以$\frac{AC}{AB}=\frac{1}{3}$.
(2) ①因为$AB=9cm$,$CB=\frac{4}{3}AB$,
$\frac{AC}{AB}=\frac{1}{3}$,
所以BC=12cm,AC=3cm.
当点D在线段AB上运动时,
BD=3tcm,AE=tcm,
所以AD=AB-BD=$(9-3t)$cm,
CE=AC-AE=$(3-t)$cm,
所以$\frac{AD}{CE}=\frac{9-3t}{3-t}=3$,
所以$\frac{AD}{CE}$的值为3.
②由C恰好为线段BD的三等分点,
当$CD=\frac{1}{3}BD$时,
因为BC=12cm,
所以$CD=\frac{1}{2}BC=6cm$,
所以BD=18cm,所以3t=18,
所以t=6,
所以AE=6cm,CE=AE-AC=3cm,
所以DE=CD-CE=3cm.
因为M,N分别是线段DE,AB的中点,
所以$DM=\frac{1}{2}DE=\frac{3}{2}cm$,$BN=\frac{1}{2}AB=\frac{9}{2}cm$,
所以$MN=BD-DM-BN=18-\frac{3}{2}-\frac{9}{2}=12(cm)$;
当$BC=\frac{1}{3}BD$时,
因为BC=12cm,
所以CD=2BC=24cm,
所以BD=36cm,所以3t=36,
所以t=12,
所以AE=12cm,CE=AE-AC=9cm,
所以DE=CD-CE=15cm.
因为M,N分别是线段DE,AB的中点,
所以$DM=\frac{1}{2}DE=\frac{15}{2}cm$,$BN=\frac{1}{2}AB=\frac{9}{2}cm$,
所以$MN=BD-DM-BN=36-\frac{15}{2}-\frac{9}{2}=24(cm)$.
综上所述,MN的长为12cm或24cm.
15. 解:
(1)补充完整图形如图.
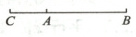
因为CB=$\frac{4}{3}AB$,
所以AC=$\frac{1}{3}AB$,
所以$\frac{AC}{AB}=\frac{1}{3}$.
(2) ①因为$AB=9cm$,$CB=\frac{4}{3}AB$,
$\frac{AC}{AB}=\frac{1}{3}$,
所以BC=12cm,AC=3cm.
当点D在线段AB上运动时,
BD=3tcm,AE=tcm,
所以AD=AB-BD=$(9-3t)$cm,
CE=AC-AE=$(3-t)$cm,
所以$\frac{AD}{CE}=\frac{9-3t}{3-t}=3$,
所以$\frac{AD}{CE}$的值为3.
②由C恰好为线段BD的三等分点,
当$CD=\frac{1}{3}BD$时,
因为BC=12cm,
所以$CD=\frac{1}{2}BC=6cm$,
所以BD=18cm,所以3t=18,
所以t=6,
所以AE=6cm,CE=AE-AC=3cm,
所以DE=CD-CE=3cm.
因为M,N分别是线段DE,AB的中点,
所以$DM=\frac{1}{2}DE=\frac{3}{2}cm$,$BN=\frac{1}{2}AB=\frac{9}{2}cm$,
所以$MN=BD-DM-BN=18-\frac{3}{2}-\frac{9}{2}=12(cm)$;
当$BC=\frac{1}{3}BD$时,
因为BC=12cm,
所以CD=2BC=24cm,
所以BD=36cm,所以3t=36,
所以t=12,
所以AE=12cm,CE=AE-AC=9cm,
所以DE=CD-CE=15cm.
因为M,N分别是线段DE,AB的中点,
所以$DM=\frac{1}{2}DE=\frac{15}{2}cm$,$BN=\frac{1}{2}AB=\frac{9}{2}cm$,
所以$MN=BD-DM-BN=36-\frac{15}{2}-\frac{9}{2}=24(cm)$.
综上所述,MN的长为12cm或24cm.
查看更多完整答案,请扫码查看


