《2025年全品学练考七年级数学上册华师大版》

12. 如图 3 - 6 - 6 所示，$A$，$B$，$C$ 三点分别代表邮局、医院、学校中的某一处，邮局和医院均在学校的北偏西方向，邮局又在医院的北偏东方向，那么图中点 $B$ 代表医院.

答案： 12. 医院

13. 如图 3 - 6 - 7.
(1)以 $B$ 为顶点的角有几个？把它们一一表示出来；
(2)指出以射线 $BA$ 为边的角；
(3)以 $D$ 为顶点，射线 $DC$ 为一边的角（小于平角）有几个？分别表示出来.

答案： 13. 解：
(1)以B为顶点的角有3个，分别是
∠ABD,∠ABC,∠DBC.
(2)以射线BA为边的角有2个，分别是
∠ABD和∠ABC.
(3)以D为顶点，射线DC为一边的角(小于平角)有2个，分别是∠BDC和∠CDE.

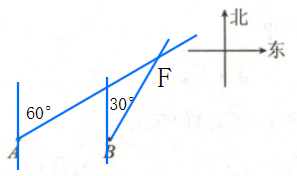
14. 如图 3 - 6 - 8，已知 $A$ 地和 $B$ 地都是海上观测站，从 $A$ 地发现它的北偏东 $60^{\circ}$方向有一艘船，同时，从 $B$ 地发现这艘船在它的北偏东 $30^{\circ}$方向，试在图中确定这艘船的位置.

答案：
14. 解：如图所示，点F即为船所在位置

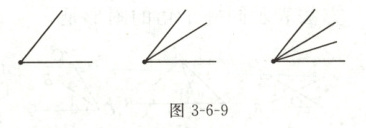
15. 新考法 探究性 (1)如图 3 - 6 - 9，有公共顶点的 2 条射线最多可以组成1个小于平角的角；
有公共顶点的 3 条射线最多可以组成3个小于平角的角；
有公共顶点的 4 条射线最多可以组成6个小于平角的角；
……
有公共顶点的 $n(n\geq2)$条射线最多可以组成\frac12n(n-1)个小于平角的角.
(2)请你写出一个学过的知识里满足类似规律的知识.

答案： 15. 解：
(1)有公共顶点的2条射线最多可以组成1个小于平角的角；
有公共顶点的3条射线最多可以组成1+2=3(个)小于平角的角；
有公共顶点的4条射线最多可以组成1+2+3=6(个)小于平角的角；
······
有公共顶点的n(n≥2)条射线最多可以组成$\frac{1}{2}n(n-1)$个小于平角的角.
故答案为$1,3,6,\frac12n(n-1).$
(2)答案不唯一，如平面上有n(n≥2)个点，
最多能画出$\frac12n(n-1)$条直线；直线l上有
n(n≥2)个点，一共有$\frac12n(n-1)$条线段.