《2025年全品学练考七年级数学上册华师大版》

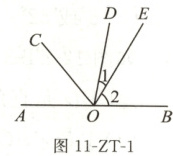
1. 如图 11-ZT-1，已知 $ O $ 为直线 $ AB $ 上一点，过点 $ O $ 在直线 $ AB $ 的同侧作三条射线 $ OC $，$ OD $，$ OE $，且 $ OC $ 是 $ \angle AOD $ 的平分线，$ \angle 2 = 3\angle 1 $，$ \angle COE = 70^{\circ} $，求 $ \angle 2 $ 的度数。

答案： 1. $60^{\circ}$

2. $ OC $，$ OD $ 是从 $ \angle AOB $ 的顶点 $ O $ 引出的两条射线，若 $ \angle AOB = 75^{\circ} $，$ \angle BOC = 45^{\circ} $，并且 $ OD $ 平分 $ \angle AOC $，试求 $ \angle BOD $ 的度数。

答案： 2. $60^{\circ}$或$15^{\circ}$

3. 已知 $ \angle COD = 30^{\circ} $，$ \angle AOC = 90^{\circ} $，$ \angle BOD = 80^{\circ} $，$ OM $ 平分 $ \angle AOD $，$ ON $ 平分 $ \angle BOC $，求 $ \angle MON $ 的度数。

答案：
3. 解:分情况讨论:
(1)如图①所示，$\angle AOD = \angle AOC + \angle COD = 90^{\circ} + 30^{\circ} = 120^{\circ}$.
　　　　　
　　因为 OM 平分$\angle AOD$，
　所以$\angle AOM = \frac{1}{2} \angle AOD = \frac{1}{2} × 120^{\circ} = 60^{\circ}$.
　又因为$\angle AOB = \angle AOD - \angle BOD = 120^{\circ} - 80^{\circ} = 40^{\circ}$，
　　所以$\angle BOM = \angle AOM - \angle AOB = 60^{\circ} - 40^{\circ} = 20^{\circ}$.
　　因为$\angle BOD = 80^{\circ}$，$\angle COD = 30^{\circ}$，
　　所以$\angle BOC = 80^{\circ} - 30^{\circ} = 50^{\circ}$.
　　因为 ON 平分$\angle BOC$，
　　所以$\angle BON = \frac{1}{2} \angle BOC = 25^{\circ}$，
　　所以$\angle MON = \angle BON - \angle BOM = 25^{\circ} - 20^{\circ} = 5^{\circ}$;
(2)如图②所示.
　　　　　
　因为$\angle COD = 30^{\circ}$，$\angle AOC = 90^{\circ}$，
　所以$\angle AOD = \angle COD + \angle AOC = 30^{\circ} + 90^{\circ} = 120^{\circ}$.
　因为 OM 平分$\angle AOD$，
　所以$\angle AOM = \frac{1}{2} \angle AOD = 60^{\circ}$，
　所以$\angle MOC = \angle AOC - \angle AOM = 30^{\circ}$.
　因为$\angle BOD = 80^{\circ}$，
　所以$\angle BOC = \angle BOD + \angle COD = 80^{\circ} + 30^{\circ} = 110^{\circ}$.
　因为 ON 平分$\angle BOC$，
　所以$\angle CON = \frac{1}{2} \angle BOC = \frac{1}{2} × 110^{\circ} = 55^{\circ}$，
　所以$\angle MON = \angle MOC + \angle CON = 30^{\circ} + 55^{\circ} = 85^{\circ}$;
(3)如图③所示
　　　　　
　　　　　
　易得$\angle MON = \angle DOM + \angle COD + \frac{1}{2} \angle BOC = \frac{1}{2} (\angle AOC - \angle COD) + 30^{\circ} + \frac{1}{2} (\angle BOD - \angle COD) = 30^{\circ} + 30^{\circ} + 25^{\circ} = 85^{\circ}$;
(4)如图④所示
　易得$\angle MON = \angle COM - \angle CON = (\angle COD + \angle DOM) - \frac{1}{2} \angle BOC = (30^{\circ} + \frac{1}{2} \angle AOD) - \frac{1}{2} (\angle BOD + \angle COD) = [30^{\circ} + \frac{1}{2} (\angle AOC - \angle COD)] - \frac{1}{2} × (80^{\circ} + 30^{\circ}) = 60^{\circ} - 55^{\circ} = 5^{\circ}$.
　综上所述，$\angle MON$的度数为$5^{\circ}$或$85^{\circ}$.

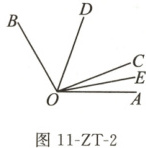
4. 已知 $ \angle AOC $ 和 $ \angle BOC $，$ OD $ 平分 $ \angle BOC $，$ OE $ 平分 $ \angle AOC $。
（1）请写出一对相等的角；
（2）若 $ \angle AOC $ 在 $ \angle BOC $ 的外部，且 $ \angle AOB = 120^{\circ} $，如图 11-ZT-2，其他条件不变，求 $ \angle DOE $ 的度数；
（3）若 $ \angle AOC = \alpha $，$ \angle BOC = \beta $（$ \alpha $，$ \beta $ 都大于 $ 0^{\circ} $ 小于 $ 180^{\circ} $，且 $ \alpha ＜ \beta $），其他条件不变，试求 $ \angle DOE $ 的度数（结果用含 $ \alpha $，$ \beta $ 的代数式表示）。

答案：
4. 解:
(1)$\angle AOE = \angle COE$或$\angle BOD = \angle DOC$(答案不唯一，写出一对即可).
(2)因为 OE 平分$\angle AOC$(已知)，
　　所以$\angle COE = \frac{1}{2} \angle AOC$(角平分线的定义).
　同理，$\angle DOC = \frac{1}{2} \angle BOC$，
　　所以$\angle DOE = \angle DOC + \angle COE = \frac{1}{2} \angle BOC + \frac{1}{2} \angle AOC = \frac{1}{2} \angle AOB$.
　　因为$\angle AOB = 120^{\circ}$(已知)，
　　所以$\angle DOE = 60^{\circ}$.
(3)①若$\angle AOC$在$\angle BOC$的外部，由
(2)得$\angle DOE = \frac{1}{2} (\alpha + \beta)$;
　　②若$\angle AOC$在$\angle BOC$的内部，如图.
　　　　　　
　　因为 OE 平分$\angle AOC$(已知)，
　　所以$\angle COE = \frac{1}{2} \angle AOC = \frac{1}{2} \alpha$(角平分线的定义).
　　同理，$\angle DOC = \frac{1}{2} \angle BOC = \frac{1}{2} \beta$，
　　所以$\angle DOE = \angle DOC - \angle COE = \frac{1}{2} (\beta - \alpha)$.
　综上所述，$\angle DOE$的度数为$\frac{1}{2} (\alpha + \beta)$或$\frac{1}{2} (\beta - \alpha)$.