《2025年全品学练考七年级数学上册华师大版》

14. 数学思想 数形结合 已知 a，b 在数轴上的对应点的位置如图 1 - 3 - 3 所示.
(1)找出数 a，b 的相反数在数轴上的对应点的位置；
(2)若数 b 与其相反数相距 10 个单位长度，则数 b 表示的数是-5；
(3)在(2)的条件下，若表示数 a 的点与表示数 b 的相反数的点相距 2 个单位长度，则数 a 表示的数是3.
]

答案：
14. 解：
(1)如图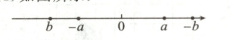所示.
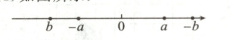
(2)-5
(3)3

15. 已知 a 是$-[-(-5)]$的相反数，b 比最小的正整数大 4，c 是相反数为它本身的数，计算$3a + 4b + 5c$的值.

答案： 15. 35

16. (1)化简下列各式，并回答问题：
$-(-2)=$2；
$+(-\frac{1}{3})=$$-\frac{1}{3}$；
$-[-(-5)]=$-5；
$-[-(+4)]=$4；
$-\{+[-(-6)]\}=$-6.
(2)当$+5$前面有 99 个负号时，化简后的结果是-5；当$+5$前面有 100 个负号时，化简后的结果是5. 你能总结出什么规律？
(3)计算：
$\underbrace{-\{ -[-·s -(-6)]\} }_{2n个负号,n为正整数}+\underbrace{-\{ -[-·s -(-6)]\} }_{(2n - 1)个负号,n为正整数}$.

答案： 16. 解：
(1)2 $-\frac{1}{3}$ -5 4 -6
(2)-5 5
规律：当一个正数前面有奇数个负号时,化简后的结果为负，当一个正数前面有偶数个负号时,化简后的结果为正.
(3)原式=6+(-6)=0.