《2025年全品学练考七年级数学上册华师大版》

1. 在代数式 $3\pi$，$2a + b$，$\frac{3}{7}x^{2}$，$\frac{6}{m}$，$-m$，$0$，$\frac{a + b}{2a - b}$，$\frac{5x - 4y}{3}$，$60\%y$ 中，单项式的个数是(C)

A.7
B.6
C.5
D.4

答案： 1. C

2. 单项式 $-4\pi xy^{2}z^{3}$ 的系数和次数分别是(D)

A.$-4$，7
B.$-\pi$，5
C.$-4$，6
D.$-4\pi$，6

答案： 2. D

3. 下列说法错误的个数是(B)
① $-\frac{ab^{2}}{3}$ 是单项式；②单项式 $a$ 没有系数，也没有次数；③ $0$ 不是单项式；④ $\frac{m}{5}$ 与 $\frac{5}{m}$ 都是单项式；⑤ $\frac{x + y}{2}$ 是单项式；⑥ $-\pi x$ 的系数为 $-1$；⑦ $-5a^{2}b$ 的次数是 3.

A.4
B.5
C.6
D.7

答案： 3. B

4. 若 $3a^{2}b^{m + 1}$ 是五次单项式，则 $m =$2.

答案： 4. 2

5. 写出下列各单项式的系数和次数：

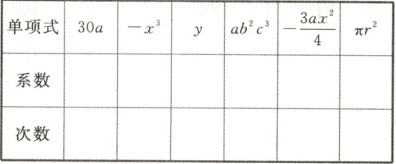
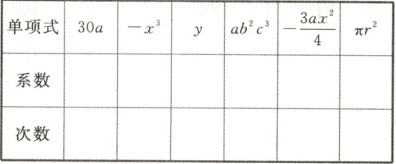
答案： 5. 解：表格第二行从左到右依次填：30，-1，1，1，$-\frac{3}{4}，$$\pi.$
表格第三行从左到右依次填：1，3，1，6，3，2.

6. 如果单项式 $3a^{2}b^{3m - 4}$ 的次数与单项式 $\frac{1}{3}x^{3}y^{2}z^{2}$ 的次数相同，则 $m$ 的值为(B)

A.2
B.3
C.4
D.5

答案： 6. B

7. (1)写出一个系数是 2024，且只含有 $x$，$y$ 两个字母的三次单项式：2024xy²；
(2)写出所有只含有字母 $a$，$x$，且系数为 $-1$ 的三次单项式：-ax²，-a²x；
(3)写出所有只含有字母 $a$，$b$，$c$，且系数为 1 的四

次

单项式：a²bc，ab²c，abc².

答案： 7.
(1)答案不唯一，如$2024xy^{2}$
$(2)-ax^{2}，$$-a^{2}x (3)a^{2}bc，$$ab^{2}c，$$abc^{2}$

8. 若 $mx^{2}y^{n}z^{2}$ 是关于 $x$，$y$，$z$ 的一个单项式，且系数为 $-3$，次数为 8，则 $m =$-3，$n =$4.

答案： 8. -3 4

9. 已知 $(m + n)x^{2}y^{n + 1}$ 是关于 $x$，$y$ 的五次单项式，且系数为 6，试求 $m$，$n$ 的值.

答案： 9. m = 4 n = 2

10. 新考法 探究性 按照规律填上所缺的单项式，并回答问题：
(1)$a$，$-2a^{2}$，$3a^{3}$，$-4a^{4}$，5a⁵，-6a⁶；
(2)试写出第 2024 个和第 2025 个单项式；
(3)试写出第 $n$($n$ 为正整数)个单项式；
(4)当 $a = -1$ 时，求 $a + (-2a^{2}) + 3a^{3} + (-4a^{4}) + ·s + 99a^{99} + (-100a^{100})$ 的值.

答案： 10. 解：$(1)5a^{5} -6a^{6}$
(2)第2024个单项式为$-2024a^{2024}，$第2025个单项式为$2025a^{2025}.$
(3)第n个单项式为$(-1)^{n + 1}na^{n}.$
(4)原式=-1 -2 -3 - ·s -100 = -5050.