第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 如图 9-ZT-1,点 C 在线段 AB 上,$AC = 8\mathrm{cm}$,$CB = 6\mathrm{cm}$,M,N 分别是 AC,BC 的中点,线段 MN 的长为

7 cm
。
答案:
1. 7 cm
2. 数学思想 数形结合 如图 9-ZT-2,点 C 在线段 AB 上,M,N 分别是 AC,BC 的中点。
(1) 若$AC = 9\mathrm{cm}$,$BC = 6\mathrm{cm}$,求线段 MN 的长;
(2) 若 C 为线段 AB 上任意一点,且满足$AC + BC = a\mathrm{cm}$,其他条件不变,你能猜想 MN 的长度吗?请你说明理由。你能用一句简洁的话描述你发现的结论吗?
(3) 若点 C 在线段 AB 的延长线上,且满足$AC - BC = b\mathrm{cm}$,M,N 分别为 AC,BC 的中点,你能猜想 MN 的长度吗?请画出图形,写出你的结论,并说明理由。

(1) 若$AC = 9\mathrm{cm}$,$BC = 6\mathrm{cm}$,求线段 MN 的长;
(2) 若 C 为线段 AB 上任意一点,且满足$AC + BC = a\mathrm{cm}$,其他条件不变,你能猜想 MN 的长度吗?请你说明理由。你能用一句简洁的话描述你发现的结论吗?
(3) 若点 C 在线段 AB 的延长线上,且满足$AC - BC = b\mathrm{cm}$,M,N 分别为 AC,BC 的中点,你能猜想 MN 的长度吗?请画出图形,写出你的结论,并说明理由。

答案:
2. 解:
(1)因为$AC = 9$ cm,M是AC的中点,
所以$CM=\frac{1}{2}AC=\frac{1}{2}×9 = 4.5(cm)$。
因为$BC = 6$ cm,N是BC的中点,
所以$CN=\frac{1}{2}BC=\frac{1}{2}×6 = 3(cm)$,
所以$MN = CM + CN = 4.5 + 3 = 7.5(cm)$。
故线段MN的长为7.5 cm。
(2)猜想:$MN=\frac{1}{2}a$ cm。
理由:因为M,N分别是AC,BC的中点,
所以$CM=\frac{1}{2}AC,CN=\frac{1}{2}BC$,
所以$MN = CM + CN=\frac{1}{2}AC+\frac{1}{2}BC=$
$\frac{1}{2}(AC + BC)=\frac{1}{2}a(cm)$。
结论:当C为线段AB上任意一点,且M,N
分别是AC,BC的中点时,$MN=\frac{1}{2}AB$。
(3)若点C在线段AB的延长线上,如图。
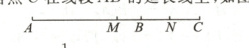
结论:$MN=\frac{1}{2}b$ cm。
理由:因为M,N分别是AC,BC的中点,
所以$CM=\frac{1}{2}AC,CN=\frac{1}{2}BC$,
所以$MN = CM - CN=\frac{1}{2}AC-\frac{1}{2}BC=$
$\frac{1}{2}(AC - BC)=\frac{1}{2}b(cm)$。
2. 解:
(1)因为$AC = 9$ cm,M是AC的中点,
所以$CM=\frac{1}{2}AC=\frac{1}{2}×9 = 4.5(cm)$。
因为$BC = 6$ cm,N是BC的中点,
所以$CN=\frac{1}{2}BC=\frac{1}{2}×6 = 3(cm)$,
所以$MN = CM + CN = 4.5 + 3 = 7.5(cm)$。
故线段MN的长为7.5 cm。
(2)猜想:$MN=\frac{1}{2}a$ cm。
理由:因为M,N分别是AC,BC的中点,
所以$CM=\frac{1}{2}AC,CN=\frac{1}{2}BC$,
所以$MN = CM + CN=\frac{1}{2}AC+\frac{1}{2}BC=$
$\frac{1}{2}(AC + BC)=\frac{1}{2}a(cm)$。
结论:当C为线段AB上任意一点,且M,N
分别是AC,BC的中点时,$MN=\frac{1}{2}AB$。
(3)若点C在线段AB的延长线上,如图。
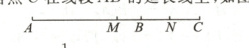
结论:$MN=\frac{1}{2}b$ cm。
理由:因为M,N分别是AC,BC的中点,
所以$CM=\frac{1}{2}AC,CN=\frac{1}{2}BC$,
所以$MN = CM - CN=\frac{1}{2}AC-\frac{1}{2}BC=$
$\frac{1}{2}(AC - BC)=\frac{1}{2}b(cm)$。
3. 如图 9-ZT-3,已知线段$AB = 20\mathrm{cm}$,延长 AB 至点 C,使得$BC = \dfrac{1}{2}AB$。
(1) 求 AC 的长;
(2) 若 D 是 AB 的中点,E 是 AC 的中点,求 DE 的长。

(1) 求 AC 的长;
(2) 若 D 是 AB 的中点,E 是 AC 的中点,求 DE 的长。

答案:
3.
(1)30 cm
(2)5 cm
(1)30 cm
(2)5 cm
4. 【问题背景】
如图 9-ZT-4,已知 D 为线段 AB 的中点,点 C 在线段 AB 上(不与点 A,B 重合)。
【初步探究】
(1) 如图①,若$AC = 8$,$BC = 6$,则线段 CD 的长为
(2) 如图①,若$AB = 18$,$BC = 2CD$,求 BC 的长;
【拓展提升】
(3) 如图②,若$BC = 2CD$,E 为 BD 的中点,$CE = 2$,求线段 AB 的长。
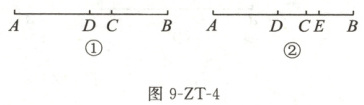
如图 9-ZT-4,已知 D 为线段 AB 的中点,点 C 在线段 AB 上(不与点 A,B 重合)。
【初步探究】
(1) 如图①,若$AC = 8$,$BC = 6$,则线段 CD 的长为
1
;(2) 如图①,若$AB = 18$,$BC = 2CD$,求 BC 的长;
【拓展提升】
(3) 如图②,若$BC = 2CD$,E 为 BD 的中点,$CE = 2$,求线段 AB 的长。

答案:
4.
(1)1
(2)6
(3)24
(1)1
(2)6
(3)24
查看更多完整答案,请扫码查看


