《2025年全品学练考七年级数学上册华师大版》

9. 如图 3 - 5 - 8，已知平面上有四个村庄，用四个点 $ A $，$ B $，$ C $，$ D $ 表示.
(1) 作直线 $ BC $ 与射线 $ AD $ 交于点 $ E $；
(2) 若要建一供电所 $ M $，向四个村庄供电，要使所用电线最短，则供电所 $ M $ 应建在何处？请画出点 $ M $ 的位置并说明理由.

答案：
9.解:
(1)如图:
　　　　　
(2)如图所示，连结AC，BD交于点M，点M即为所求.
　　　　　　
　　理由:两点之间，线段最短.

10. 如图 3 - 5 - 9，平面内有三个点，过其中任意两点画直线，有如下两种情况：
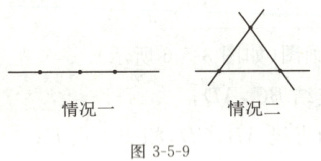
(1) 若平面内有四个点，过其中任意两点画直线，有多少种情况？请画图说明；
(2) 若平面内有 6 个点，过其中任意两点画直线，最多可以画多少条直线？
(3) 若平面内有 $ n $ 个点，过其中任意两点画直线，最多可以画多少条直线？（直接写出结果）

答案：
10.解:
(1)如图所示，一共有三种情况:
　　　
(2)画直线条数最多的情况为任意三点均不共线，
　　所以平面内有6个点，过其中任意两点最多画$\frac{6×(6 - 1)}{2}=15$(条)直线
(3)最多可以画$\frac{n(n - 1)}{2}$条直线.

11. 新考法 探究性 阅读：在直线上有 $ n $ 个不同的点，则此图中共有多少条线段？通过分析、画图尝试得到如下表格：

回答下列问题：
(1) 把表格补充完整.
(2) ①某学校七年级共有 20 个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛共要进行多少场？
②乘火车从 $ A $ 站出发，沿途经过 10 个车站方可到达 $ B $ 站，那么在 $ A $，$ B $ 两站之间需要安排多少种不同的车票？

答案： 11.解:
(1)$\frac{n(n - 1)}{2}$
　　$0 + 1 + 2 + 3 + ·s + (n - 1) = \frac{n(n - 1)}{2}$
(2)①把每一个班看作一个点，则$\frac{20×(20 - 1)}{2}=190$(场).
　　故该校七年级的辩论赛共要进行190场.②由题意可得一共有12个车站，看作12个点，线段条数为$\frac{12×11}{2}=66$(条).
　　因为车票有出发站和到达站之分，
　　所以不同的车票要安排$2×66 = 132$(种).