第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 新情境 中华传统文化 (2024 河北)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图 6-ZT-1 所示的“表格算法”,图①表示 $132×23$,运算结果为 3036. 图②表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图②中现有数据进行推断,正确的是 (
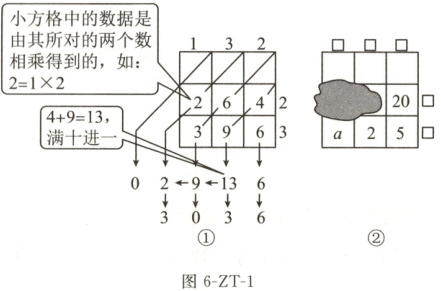
A.“20”左边的数是 16
B.“20”右边的“□”表示 5
C.运算结果小于 6000
D.运算结果可以表示为 $4100a+1025$
D
)
A.“20”左边的数是 16
B.“20”右边的“□”表示 5
C.运算结果小于 6000
D.运算结果可以表示为 $4100a+1025$
答案:
1.D
2. 一个三位数 $M$,百位数字为 $a$,十位数字为 $b$,个位数字是 $c$.
(1) 请用含 $a$,$b$,$c$ 的式子表示这个数 $M$;
(2) 现在把三位数 $M$ 的百位数字、十位数字、个位数字分别交换到个位数字、百位数字、十位数字,得到一个新的三位数 $N$,请用含 $a$,$b$,$c$ 的式子表示 $N$;
(3) 请用含 $a$,$b$,$c$ 的式子表示 $N - M$,请判断 $N - M$ 是否能被 9 整除,并说明理由.
(1) 请用含 $a$,$b$,$c$ 的式子表示这个数 $M$;
(2) 现在把三位数 $M$ 的百位数字、十位数字、个位数字分别交换到个位数字、百位数字、十位数字,得到一个新的三位数 $N$,请用含 $a$,$b$,$c$ 的式子表示 $N$;
(3) 请用含 $a$,$b$,$c$ 的式子表示 $N - M$,请判断 $N - M$ 是否能被 9 整除,并说明理由.
答案:
2.解:(1)因为一个三位数M,百位数字为a,十位数字为b,个位数字是c,
所以M为100a+10b+c.
(2)由题意,一个新的三位数N,其百位数字是b,十位数字是c,个位数字是a,
所以N为100b+10c+a.
(3)N−M能被9整除.理由如下:
N−M=(100b+10c+a)−(100a+10b+c)
=100b+10c+a−100a−10b−c
=−99a+90b+9c
=9(−11a+10b+c).
又因为a,b,c均为整数,
所以N−M能被9整除.
所以M为100a+10b+c.
(2)由题意,一个新的三位数N,其百位数字是b,十位数字是c,个位数字是a,
所以N为100b+10c+a.
(3)N−M能被9整除.理由如下:
N−M=(100b+10c+a)−(100a+10b+c)
=100b+10c+a−100a−10b−c
=−99a+90b+9c
=9(−11a+10b+c).
又因为a,b,c均为整数,
所以N−M能被9整除.
3. 新考法 跨学科 “柳庭风静人眠昼,昼眠人静风庭柳”,从左向右读与从右向左读完全相同,这样的诗称为回文诗. 在数学中也有这样的一类数. 一个自然数从左向右读与从右向左读完全相等,这样的数称为回文数,如 121 与 1221 均为回文数. 回文数与其各个数位上的数字之和的差值称为回自差,如 121 的回自差为 $121-(1 + 2 + 1)=117$.
(1) 请你直接写出最小的三位回文数,并求其回自差;
(2) 任意三位回文数的回自差最大能被哪个正整数整除?请你说明理由;
(3) 任意四位回文数的回自差最大能被正整数
(1) 请你直接写出最小的三位回文数,并求其回自差;
(2) 任意三位回文数的回自差最大能被哪个正整数整除?请你说明理由;
(3) 任意四位回文数的回自差最大能被正整数
27
整除.
答案:
3.解:(1)由条件可知最小的三位回文数为101,其回自差为101−(1+0+1)=99.
(2)任意三位回文数的回自差最大能被9整除.理由如下:
设一个三位回文数为aba(a≠0).
其中a,b都为不超过9的自然数,则该三位回文数为100a+10b+a=101a+10b,
所以该三位回文数的回自差为101a+10b−(a+b+a)=9(11a+b).
由条件可知11a+b是整数,
所以该三位回文数的回自差一定是9的倍数,
所以任意三位回文数的回自差最大能被9整除.
(3)设该四位回文数的千位数字为x,百位数字为y,则该四位回文数为1000x+100y+10y+x=1001x+110y,
所以该四位回文数的回自差为1001x+110y−(x+y+y+x)=999x+108y=27(37x+4y),
由条件可知37x+4y是整数,
所以该四位回文数的回自差一定是27的倍数,
所以任意四位回文数的回自差最大能被27整除.
故答案为27.
(2)任意三位回文数的回自差最大能被9整除.理由如下:
设一个三位回文数为aba(a≠0).
其中a,b都为不超过9的自然数,则该三位回文数为100a+10b+a=101a+10b,
所以该三位回文数的回自差为101a+10b−(a+b+a)=9(11a+b).
由条件可知11a+b是整数,
所以该三位回文数的回自差一定是9的倍数,
所以任意三位回文数的回自差最大能被9整除.
(3)设该四位回文数的千位数字为x,百位数字为y,则该四位回文数为1000x+100y+10y+x=1001x+110y,
所以该四位回文数的回自差为1001x+110y−(x+y+y+x)=999x+108y=27(37x+4y),
由条件可知37x+4y是整数,
所以该四位回文数的回自差一定是27的倍数,
所以任意四位回文数的回自差最大能被27整除.
故答案为27.
查看更多完整答案,请扫码查看


