第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
10. 如图 3 - 6 - 18,将一块透明三角板中$60^{\circ}$角的顶点与另一块透明三角板的直角顶点重合,若$\angle 1 = 24^{\circ}10'$,则$\angle 2$的度数是(
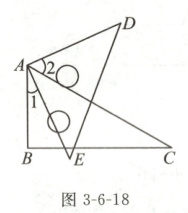
A.$34^{\circ}50'$
B.$54^{\circ}10'$
C.$65^{\circ}50'$
D.$25^{\circ}10'$
B
)
A.$34^{\circ}50'$
B.$54^{\circ}10'$
C.$65^{\circ}50'$
D.$25^{\circ}10'$
答案:
10. B
11. 如图 3 - 6 - 19,$\angle AOB = 60^{\circ}$,射线$OC$平分$\angle AOB$,以$OC$为一边作$\angle COP = 15^{\circ}$,则$\angle BOP$的度数为(
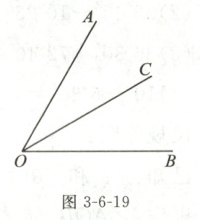
A.$15^{\circ}$
B.$45^{\circ}$
C.$15^{\circ}$或$30^{\circ}$
D.$15^{\circ}$或$45^{\circ}$
D
)
A.$15^{\circ}$
B.$45^{\circ}$
C.$15^{\circ}$或$30^{\circ}$
D.$15^{\circ}$或$45^{\circ}$
答案:
11. D
12. 如图 3 - 6 - 20,$\angle AOB=\frac{1}{2}\angle BOC$,$\angle COD=\angle AOD = 3\angle AOB$,则$\angle BOD$的度数是(
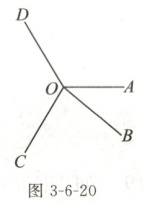
A.$160^{\circ}$
B.$150^{\circ}$
C.$120^{\circ}$
D.$100^{\circ}$
A
)
A.$160^{\circ}$
B.$150^{\circ}$
C.$120^{\circ}$
D.$100^{\circ}$
答案:
12. A
13. 在所给的:①$15^{\circ}$,②$65^{\circ}$,③$75^{\circ}$,④$135^{\circ}$,⑤$145^{\circ}$的角中,可以用一副三角板画出来的是(
A.②④⑤
B.①②④
C.①③⑤
D.①③④
D
)A.②④⑤
B.①②④
C.①③⑤
D.①③④
答案:
13. D
14. 计算:(1)$30^{\circ}30'×3$;(2)$15^{\circ}30'÷5$。
答案:
14.
(1)91°30′
(2)3°6′
(1)91°30′
(2)3°6′
15. 如图 3 - 6 - 21,$O$为直线$AB$上的一点,$\angle AOC = 48^{\circ}$,$OD$平分$\angle AOC$,$\angle DOE = 90^{\circ}$。
(1)求$\angle BOD$的度数;
(2)$OE$是$\angle BOC$的平分线吗?为什么?
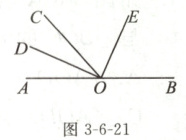
(1)求$\angle BOD$的度数;
(2)$OE$是$\angle BOC$的平分线吗?为什么?

答案:
15. 解:
(1)因为∠AOC = 48°,OD平分∠AOC,
所以$∠AOD = ∠COD = \frac{1}{2}∠AOC = 24°,$
所以∠BOD = 180° - ∠AOD = 156°。
(2)OE是∠BOC的平分线.
理由:因为∠DOE = 90°,
所以∠COD + ∠COE = 90°,
所以∠AOD + ∠BOE = 180° - ∠DOE = 90°。
又因为∠AOD = ∠COD,
所以∠COE = ∠BOE,
所以OE是∠BOC的平分线.
(1)因为∠AOC = 48°,OD平分∠AOC,
所以$∠AOD = ∠COD = \frac{1}{2}∠AOC = 24°,$
所以∠BOD = 180° - ∠AOD = 156°。
(2)OE是∠BOC的平分线.
理由:因为∠DOE = 90°,
所以∠COD + ∠COE = 90°,
所以∠AOD + ∠BOE = 180° - ∠DOE = 90°。
又因为∠AOD = ∠COD,
所以∠COE = ∠BOE,
所以OE是∠BOC的平分线.
16. 如图 3 - 6 - 22,$\angle AOB = 60^{\circ}$,图①中$\angle AOC_1=\angle C_1OB$,图②中$\angle AOC_1=\angle C_1OC_2=\angle C_2OB$,图③中$\angle AOC_1=\angle C_1OC_2=\angle C_2OC_3=\angle C_3OB$……按此规律排列下去,前 4 个图形中的$\angle AOC_1$之和为(
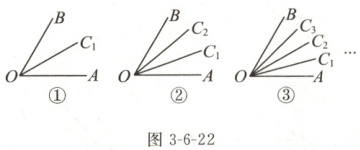
A.$60^{\circ}$
B.$67^{\circ}$
C.$77^{\circ}$
D.$87^{\circ}$
C
)
A.$60^{\circ}$
B.$67^{\circ}$
C.$77^{\circ}$
D.$87^{\circ}$
答案:
16. C
查看更多完整答案,请扫码查看


