《2025年名校课堂六年级数学上册鲁教版山东专版54制》

6. 从$2$开始，连续的偶数相加，它们和的情况如下表：

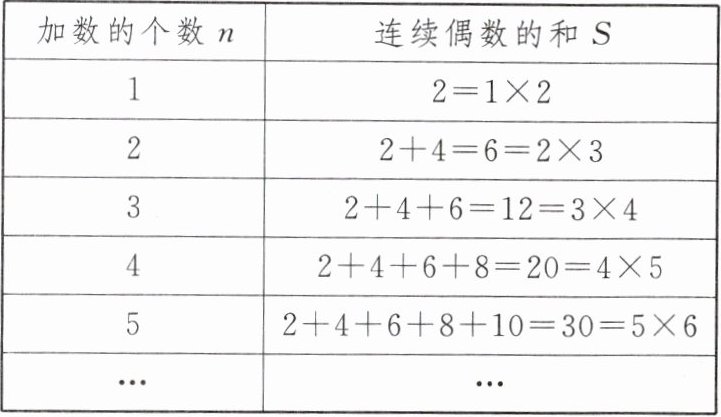
根据表中的规律猜想：用含$n$的代数式表示$S$的公式：$S = 2 + 4 + 6 + 8 + \cdots + 2n =$n(n+1)。

答案： 6.n(n+1)

7.(泰安岱岳区期末)找出下列各图形中数的规律，依此，$a$的值为226。

答案： 7.226

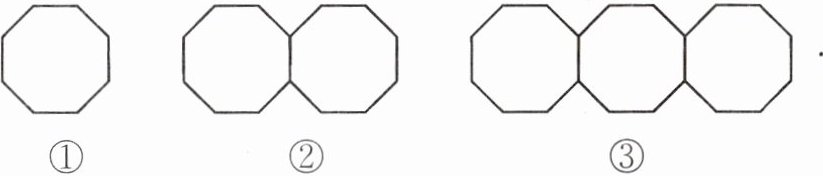
8.(宁波中考)下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需$8$根火柴棒，图案②需$15$根火柴棒，$\cdots$，按此规律，图案⑦需50根火柴棒。

答案： 8.50

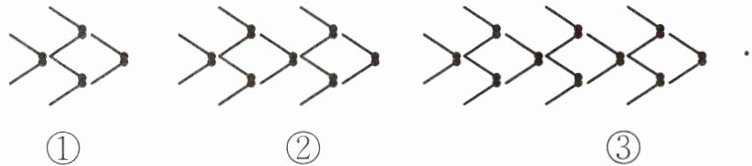
9. 如图，用火柴棒摆“金鱼”，按照这样的规律，摆第$n$条“金鱼”需用火柴棒的根数为(6n+2)。

答案： 9.(6n+2)

10.(泰安中考)将从$1$开始的连续自然数按以下规律排列，若有序数对$(n,m)$表示第$n$行，从左到右第$m$个数，如$(3,2)$表示$6$，则表示$99$的有序数对是(10,18)。

答案： 10.(10,18)

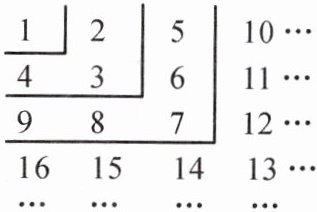
11. 将从$1$开始的自然数按以下规律排列，例如位于第$3$行、第$4$列的数是$12$，则位于第$35$行、第$6$列的数是1220。

答案： 11.1220

12. 有下列单项式：$-x$，$2x^2$，$-3x^3$，$4x^4$，$\cdots$，$-19x^{19}$，$20x^{20}$，$\cdots$。
（1）你能发现它们的排列规律吗？
（2）根据你发现的规律，写出第$2024$，$2023$个单项式。

答案： 12.解：
(1)由单项式：$-x,2x^{2},-3x^{3},4x^{4},…,-19x^{19},20x^{20},…$规律可得，第n项为$(-1)^{n}nx^{n}.(2)$第2024,2023个单项式分别为$2024x^{2024},-2023x^{2023}.$

13.(东营广饶县期末)如图所示的是某年$10$月的月历，用如图所示的“凹”字形在月历中任意圈出$5$个数，设“凹”字形框中的五个数分别$a_1$，$a_2$，$a$，$a_3$，$a_4$。

(1)直接写出$a_1 =$a-8，$a_3 =$a+1，(用含$a$的式子表示)$a_4 - a_2 =$-5；
(2)在移动“凹”字形框过程中，小明说被框住的$5$个数字之和可能为$106$，小敏说被框住的$5$个数字之和可能为$90$，你同意他们的说法吗？请说明理由；
(3)若另一个“凹”字形框框住的五个数分别为$b_1$，$b_2$，$b$，$b_3$，$b_4$，且$b = 2a + 1$，则符合条件的$b$的值为21,23或29。

答案： 13.解：
(1)a-8 a+1 -5
(2)同意小明的说法.理由：小明：(a-8)+(a-1)+a+(a+1)+(a-6)=5a-14=106，所以a=24.小敏：(a-8)+(a-1)+a+(a+1)+(a-6)=5a-14=90，所以a=20.8(不符合题意，舍去).所以小明的说法对，小敏的说法不对.
(3)21,23或29