《2025年名校课堂六年级数学上册鲁教版山东专版54制》

【例1】小刚的家离学校1500米，他每天步行上学，速度为$v$米/分.
(1) 小刚从家到学校需要\frac{1500}{v}分钟；
(2) 小刚是周二的值日生，这天早晨为了提前到校做好值日，他需要比平时每分钟多走20米. 这一天小刚从家到学校需要\frac{1500}{v+20}分钟，他比平时早到校\frac{1500}{v}-\frac{1500}{v+20}分钟.

答案： $(1)\frac{1500}{v}(2)\frac{1500}{v+20}(3)\frac{1500}{v}-\frac{1500}{v+20}$

【跟踪训练1】工程队计划修建一条长$m$米的公路，采取新的施工方式后，实际每天修建公路的长度比原计划增加15米，从而缩短了工期，设原计划每天修建公路$x$米.
(1) 原计划修建这条公路需要\frac{m}{x}天，实际修建这条公路用了\frac{m}{x+15}天；
(2) 实际修建这条公路的工期比原计划缩短了\frac{m}{x}-\frac{m}{x+15}天.

答案： $(1)\frac{m}{x}\frac{m}{x+15}(2)(\frac{m}{x}-\frac{m}{x+15})$

【例2】请你用实例解释下列代数式的意义：
(1)$5a + 10b$；
(2)$3x$.
【解答】

答案：
(1)答案不唯一，如：5a+10b表示每支笔a元，每本笔记本b元，5支笔与10本笔记本需多少元.
(2)答案不唯一，如：3x表示一辆车行驶速度为xkm/h，3小时行驶多少千米.

【跟踪训练2】代数式$5m + 2$的实际意义可表示为油箱里有2升油，加油时每分钟可以注入5升油，则m分钟后油箱中油的升数.

答案： 答案不唯一，如：油箱里有2升油，加油时每分钟可以注入5升油，则m分钟后油箱中油的升数

1. 下列解释$3a$表示的意义不正确的是(D)

A.如果橘子的价格是3元/千克，那么$3a$表示买$a$千克橘子的金额
B.如果一个等边三角形的边长为$a$，那么$3a$表示这个三角形的周长
C.如果在校平均一天的生活费用为$a$元，那么$3a$表示3天的生活费用
D.如果步行的速度为$a$米/分，那么$3a$表示步行3米所用的时间

答案： 1.D

2. 某工厂去年生产了$x$台机床，今年增长了35%，今年的产量为1.35x台.

答案： 2.1.35x

3. (长春中考)2023长春马拉松于5月21日在南岭体育场鸣枪开跑. 某同学参加了7.5千米健康跑项目，他从起点开始以平均每分钟$x$千米的速度跑了10分钟，此时他离健康跑终点的路程为7.5-10x千米.

答案： 3.(7.5-10x)

4. 联系实际背景，说明代数式$6a^{3}$的意义.

答案： 4.解：答案不唯一，如：6个棱长为a的正方体的体积之和.

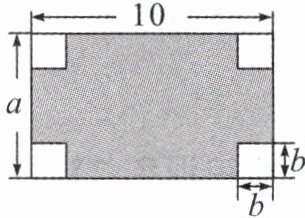
$5. $如图，把长为$10，$宽为$a$的长方形的四个角挖去边长为$b$的四个小正方形，则图中阴影部分的面积为　　$10a-4b^2$　　$.$　　

答案： $5.10a-4b^2$

$6. $甲、乙两个码头相距$s$千米，某船在静水中的速度为$a$千米$/$时，水流速度为$b$千米$/$时，则船一次往返两个码头所需的时间为　　$\frac{s}{a+b}+\frac{s}{a-b}$　　小时$.$　　

答案： $6.(\frac{s}{a+b}+\frac{s}{a-b})$

7. 试举实际例子说明下列代数式的意义：
(1)$2(x + 2)^{2}$；
(2)$\frac{2a + b}{3}$.

答案： 7.解：
(1)答案不唯一，如：$2(x+2)^2$可以解释为2个边长为x+2的正方形的面积的和.
(2)答案不唯一，如：$\frac{2a+b}{3}$可以解释为购买甲种糖果2千克，乙种糖果1千克，已知甲种糖果每千克a元，乙种糖果每千克b元，则所购买的糖果平均每千克的价格为$\frac{2a+b}{3}$元.