第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
9.(泰安岱岳区期末)化简$\frac{5}{2}xy^{2}-\frac{1}{2}(x^{2}y-5xy^{2})$的结果是(
A.$-\frac{1}{2}x^{2}y$
B.$\frac{9}{2}x^{2}y$
C.$-\frac{1}{2}x^{2}y-5xy^{2}$
D.$-\frac{1}{2}x^{2}y+5xy^{2}$
D
)A.$-\frac{1}{2}x^{2}y$
B.$\frac{9}{2}x^{2}y$
C.$-\frac{1}{2}x^{2}y-5xy^{2}$
D.$-\frac{1}{2}x^{2}y+5xy^{2}$
答案:
9.D
10. 根据去括号的法则,在方框中填上“+”或“—”,正确的是(
①$2x□(-y+2x)=4x-y$;
②$(x^{2}+2y^{2})□(x^{2}+y^{2})=y^{2}$;
③$-(2x+3y)□(x-3y)=-3x$;
④$a□(m+n-p+d)=a-m-n+p-d$。
A.$+,+,-,-$
B.$+,-,+,-$
C.$+,-,-,+$
D.$+,-,-,-$
D
)①$2x□(-y+2x)=4x-y$;
②$(x^{2}+2y^{2})□(x^{2}+y^{2})=y^{2}$;
③$-(2x+3y)□(x-3y)=-3x$;
④$a□(m+n-p+d)=a-m-n+p-d$。
A.$+,+,-,-$
B.$+,-,+,-$
C.$+,-,-,+$
D.$+,-,-,-$
答案:
10.D
11.(泰安新泰市期末)已知$a,b$在数轴上的位置如图所示,化简$|a|-|a-b|+|a+b|$的结果为(
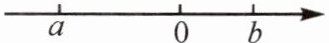
A.$a-2b$
B.$-a-2b$
C.$-3a$
D.$-3a+2b$
B
)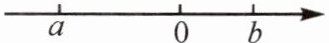
A.$a-2b$
B.$-a-2b$
C.$-3a$
D.$-3a+2b$
答案:
11.B
12.(泰安东平县期末)长方形的宽为$2a+b$,长比宽长$a-b$,则周长为(
A.$5a+b$
B.$10a+2b$
C.$7a+b$
D.$10a+b$
B
)A.$5a+b$
B.$10a+2b$
C.$7a+b$
D.$10a+b$
答案:
12.B
13.【整体思想】(东营垦利区期末)若$x+y=3$,$xy=2$,则$(4x+2)-(3xy-4y)=$
8
。
答案:
13.8
14. 化简:
(1)$2a-(3a+4b)+(2a+b)$;
(2)$3(2mn-m^{2}+n^{2})-4(mn+m^{2}+2n^{2})$。
(1)$2a-(3a+4b)+(2a+b)$;
(2)$3(2mn-m^{2}+n^{2})-4(mn+m^{2}+2n^{2})$。
答案:
14.
(1)原式=2a - 3a - 4b + 2a + b = a - 3b.
(2)原式=6mn - 3m² + 3n² - 4mn - 4m² - 8n² = -7m² - 5n² + 2mn.
(1)原式=2a - 3a - 4b + 2a + b = a - 3b.
(2)原式=6mn - 3m² + 3n² - 4mn - 4m² - 8n² = -7m² - 5n² + 2mn.
15. 已知$(a+2)^{2}+4|b-5|=0$,求$(7a+8b)-(-4a+6b)$的值。
答案:
15.解:根据题意,得a + 2 = 0,b - 5 = 0.解得a = -2,b = 5.原式=7a + 8b + 4a - 6b = 11a + 2b.当a = -2,b = 5时,原式=-22 + 10 = -12.
16. 有一道题“先化简,再求值:$10x^{2}-(4x^{2}+x-3)+(-5x^{2}+6x-1)-5x$,其中$x=-2$”。小芬做题时把“$x=-2$”错抄成了“$x=2$”,但她的计算结果也是正确的,请你说明这是什么原因?
答案:
16.解:原式=10x² - 4x² - x + 3 - 5x² + 6x - 1 - 5x = (10 - 4 - 5)x² + (-1 + 6 - 5)x + (3 - 1) = x² + 2.因为x = 2或x = -2时,x²的值均为4,原式的计算结果都是6.所以把“x = -2”错抄成“x = 2”,计算结果也是正确的.
17. 某公交车上原有$(4a-b)$人,中途有一半人下车,同时又有若干人上车,这时车上共有乘客$(6a+b)$人,求中途上车的人数。
答案:
17.解:6a + b - [4a - b - $\frac{1}{2}$(4a - b)] = 6a + b - (4a - b - 2a + $\frac{1}{2}$b) = 6a + b - 4a + b + 2a - $\frac{1}{2}$b = 4a + $\frac{3}{2}$b,所以中途上车的人数为(4a + $\frac{3}{2}$b)人.
查看更多完整答案,请扫码查看


