《2025年名校课堂六年级数学上册鲁教版山东专版54制》

1. 是否存在 $ m $，使关于 $ x $，$ y $ 的整式 $ (mx^{2}-x^{2}+3x + 1)-(5x^{2}-4y^{2}+3x) $ 不含 $ x^{2} $？若不存在，说明理由；若存在，求出 $ m $ 的值。

答案： 1.解：原式=mx²-x²+3x+1-5x²+4y²-3x=(m-6)x²+4y²+1.假设不含x²，那么m-6=0.所以m=6，即存在m=6使整式不含x².

2. 有一道题“求代数式的值：$ \frac{1}{4}(-4a^{2}+2a - 8b)-(\frac{1}{2}a - 2b)-a^{2} $，其中 $ a = -2 $，$ b = 2024 $”。小斌做题时把“$ b = 2024 $”错抄成“$ b = 2023 $”，但他的计算结果也是正确的，为什么？

答案： 2.解：原式$=-a²+ \frac{1}{2}a-2b- \frac{1}{2}a+2b-a²=-2a².$代数式计算结果不含b,与b的取值无关，所以小斌做题时把“b=2024”错抄成“b=2023”，他的计算结果也是正确的.

3.（泰安东平县期末）老师设计了一个数学实验，给甲、乙、丙三名同学各一张写有已化为最简的代数式的卡片，规则是两位同学的代数式相减等于第三位同学的代数式，则实验成功。甲、乙、丙的卡片如下，丙的卡片有一部分看不清楚了。

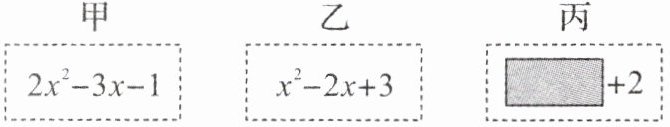
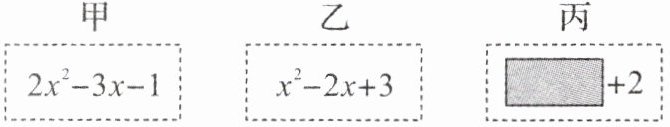
（1）计算出甲减乙的结果，并判断甲减乙能否使实验成功；
（2）嘉琪发现丙减甲可以使实验成功，请求出丙的代数式。

答案： 3.解：
(1)根据题意，得(2x²-3x-1)-(x²-2x+3)=2x²-3x-1-x²+2x-3=x²-x-4，所以甲减乙不能使实验成功.
(2)丙的代数式为2x²-3x-1+x²-2x+3=3x²-5x+2.

4.（东营垦利区期末）已知 $ A = 2x^{2}+3xy + 2y - 1 $，$ B = x^{2}-xy $。
（1）计算：$ A - 2B $；
（2）若 $ (x + 1)^{2}+|y - 2| = 0 $，求 $ A - 2B $ 的值；
（3）若 $ A - 2B $ 的值与 $ y $ 的取值无关，求 $ x $ 的值。

答案： 4.解：
(1)A-2B=2x²+3xy+2y-1-2(x²-xy)=2x²+3xy+2y-1-2x²+2xy=5xy+2y-1.
(2)因为(x+1)²+|y-2|=0，所以x=-1,y=2,则A-2B=5xy+2y-1=-10+4-1=-7.
(3)A-2B=5xy+2y-1=(5x+2)y-1.因为A-2B的值与y的取值无关，所以5x+2=0，所以$x=- \frac{2}{5}.$

5. 已知一个两位数，其十位数字是 $ a $，个位数字是 $ b $。
（1）写出这个两位数；
（2）若把这个两位数的十位数字与个位数字对换，得到一个新的两位数，这两个数的和能被 11 整除吗？为什么？

答案： 5.解：
(1)10a+b.
(2)因为(10a+b)+(10b+a)=11a+11b=11(a+b),a,b都是整数，所以a+b也是整数.所以这两个数的和能被11整除.