第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
9. 若$a = -4$,$b = -5$,$c = -7$,求式子$a - b - c$的值.
答案:
9.解:$a - b - c = (-4) - (-5) - (-7) = (-4) + 5 + 7 = 8$.
10.(淄博博山区期中)小明近期几次数学测试成绩如下:第一次$85$分,第二次比第一次高$8$分,第三次比第二次低$12$分,第四次又比第三次高$10$分,那么小明第四次测验的成绩是(
A.$90$分
B.$75$分
C.$91$分
D.$81$分
C
)A.$90$分
B.$75$分
C.$91$分
D.$81$分
答案:
10.C
11. 若$a$是最小的自然数,$b$是最大的负整数,$c$是绝对值最小的有理数,则$a - b + c=$(
A.$-1$
B.$0$
C.$1$
D.$2$
C
)A.$-1$
B.$0$
C.$1$
D.$2$
答案:
11.C
12. $-7$,$-12$,$+2$的和比它们的绝对值的和小(
A.$-38$
B.$-4$
C.$4$
D.$38$
D
)A.$-38$
B.$-4$
C.$4$
D.$38$
答案:
12.D
13. 根据如图所示的程序计算,若输入的值为$1$,则输出的值为

-5
.
答案:
13.$-5$
14. 计算:
(1)$-7.2 - 0.9 - 5.6 + 1.7$;
(2)$-7 - 4 + (-3)-(-4)+\vert -10\vert$;
(3)$(-\frac{2}{5})+(-\frac{5}{6})-(-4.9)-0.6$.
(1)$-7.2 - 0.9 - 5.6 + 1.7$;
(2)$-7 - 4 + (-3)-(-4)+\vert -10\vert$;
(3)$(-\frac{2}{5})+(-\frac{5}{6})-(-4.9)-0.6$.
答案:
14.解:
(1)原式$= -8.1 - 5.6 + 1.7 = -13.7 + 1.7 = -12$.
(2)原式$= -7 - 4 - 3 + 4 + 10 = -14 + 14 = 0$.
(3)原式$= - \frac{37}{30} + \frac{49}{10} - \frac{3}{5} = \frac{46}{15}$.
(1)原式$= -8.1 - 5.6 + 1.7 = -13.7 + 1.7 = -12$.
(2)原式$= -7 - 4 - 3 + 4 + 10 = -14 + 14 = 0$.
(3)原式$= - \frac{37}{30} + \frac{49}{10} - \frac{3}{5} = \frac{46}{15}$.
15. 小明和小红在游戏中规定:长方形表示加,圆形表示减,结果小者为胜,列式计算,小明和小红谁为胜者?


答案:
15.解:小明:$-4.5 + 3.2 - 1.1 + 1.4 = -1$,小红:$-8 + 2 - (-6) + (-7) = -7$.因为$-7 < -1$,所以小红的结果小,为胜者.
16. 若“三角” 表示运算$a - b + c$,“方框”
表示运算$a - b + c$,“方框” 表示运算$x - y + z + w$,求$\
表示运算$x - y + z + w$,求$\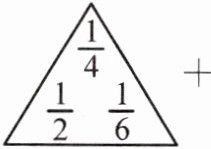

表示的运算,并计算结果.
 表示运算$a - b + c$,“方框”
表示运算$a - b + c$,“方框” 表示运算$x - y + z + w$,求$\
表示运算$x - y + z + w$,求$\

表示的运算,并计算结果.
答案:
16.解:根据题意,得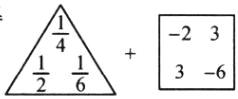
$= (\frac{1}{4} - \frac{1}{2} + \frac{1}{6}) + [(-2) - 3 + (-6) + 3] = (-\frac{1}{12}) + (-8) = -8\frac{1}{12}$.
16.解:根据题意,得
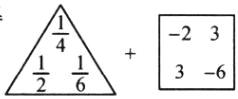
$= (\frac{1}{4} - \frac{1}{2} + \frac{1}{6}) + [(-2) - 3 + (-6) + 3] = (-\frac{1}{12}) + (-8) = -8\frac{1}{12}$.
查看更多完整答案,请扫码查看


