第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
7. 若 $a - b = 2$,$b - c = -3$,则 $a - c =$(
A.$1$
B.$-1$
C.$5$
D.$-5$
B
)A.$1$
B.$-1$
C.$5$
D.$-5$
答案:
7.B
8. (东营河口区期末)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如:$$ $-2x^{2}-2x + 1 = -x^{2}+5x - 3,$则所捂住的多项式是
$-2x^{2}-2x + 1 = -x^{2}+5x - 3,$则所捂住的多项式是
 $-2x^{2}-2x + 1 = -x^{2}+5x - 3,$则所捂住的多项式是
$-2x^{2}-2x + 1 = -x^{2}+5x - 3,$则所捂住的多项式是x²+7x−4
。
答案:
8.x²+7x−4
9. (东营垦利区期末)若关于 $a$,$b$ 的多项式 $(2a^{2}-4ab - 2b^{2})-(a^{2}+mab + 2b^{2})$ 不含 $ab$ 项,则 $m =$
−4
。
答案:
9.−4
10. 化简:
(1) $[5a^{2}-(2a - 1)]-(3 - 8a + 2a^{2})$;
(2) $3x^{2}-[7x-(4x - 3)-2x^{2}]$。
(1) $[5a^{2}-(2a - 1)]-(3 - 8a + 2a^{2})$;
(2) $3x^{2}-[7x-(4x - 3)-2x^{2}]$。
答案:
10.解:
(1)原式=5a²−2a+1−3+8a−2a²=3a²+6a−2.
(2)原式=3x²−(7x−4x+3−2x²)=3x²−7x+4x−3+2x²=5x²−3x−3.
(1)原式=5a²−2a+1−3+8a−2a²=3a²+6a−2.
(2)原式=3x²−(7x−4x+3−2x²)=3x²−7x+4x−3+2x²=5x²−3x−3.
11. (泰安东平县期末)先化简,再求值:$-(-6a^{2}b + 9ab^{2})-(5a^{2}b - 4ab^{2})$,其中 $a = 2$,$b = -1$。
答案:
11.解:原式=6a²b−9ab²−5a²b+4ab²=a²b−5ab².当a=2,b=−1 时,原式=−4−10=−14.
12. 已知某三角形的一条边长为 $m + n$,另一条边长比这条边长长 $m - 3$,第三条边长等于 $2n - m$,求这个三角形的周长。
答案:
12.解:(m+n)+(m−3)+(m+n)+(2n−m)=2m+4n−3.
13. (济宁嘉祥县期中)阅读材料:
计算 $(-3x^{3}+5x^{2}-7)+(2x - 3 + 3x^{2})$ 时,可列竖式:

小明认为,整式的加减实际上就是合并同类项,而合并同类项的关键是合并各同类项的系数,因此,可以把上题的竖式简化为:

所以原式 $= -3x^{3}+8x^{2}+2x - 10$。
根据阅读材料解答下列问题:
已知:$A = -2x - 3x^{3}+1 + x^{4}$,$B = 2x^{3}-4x^{2}+x$。
(1) 将 $A$ 按 $x$ 的降幂排列:
(2) 请仿照小明的方法计算:$A - B$;
(3) 请写出一个多项式 $C$:
计算 $(-3x^{3}+5x^{2}-7)+(2x - 3 + 3x^{2})$ 时,可列竖式:

小明认为,整式的加减实际上就是合并同类项,而合并同类项的关键是合并各同类项的系数,因此,可以把上题的竖式简化为:

所以原式 $= -3x^{3}+8x^{2}+2x - 10$。
根据阅读材料解答下列问题:
已知:$A = -2x - 3x^{3}+1 + x^{4}$,$B = 2x^{3}-4x^{2}+x$。
(1) 将 $A$ 按 $x$ 的降幂排列:
x⁴−3x³−2x+1
;(2) 请仿照小明的方法计算:$A - B$;
(3) 请写出一个多项式 $C$:
-2x³+1
,使其与 $B$ 的和是二次三项式。
答案:
13.解:
(1)A=x⁴−3x³−2x+1
(2)列竖式如下:
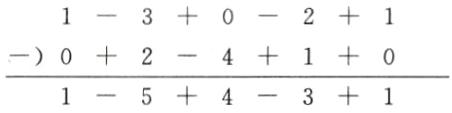
所以A - B=x⁴−5x³+4x²−3x+1.
(3)-2x³+1(答案不唯一)
13.解:
(1)A=x⁴−3x³−2x+1
(2)列竖式如下:
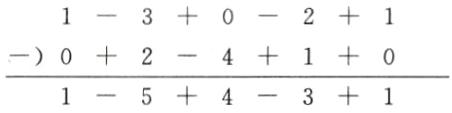
所以A - B=x⁴−5x³+4x²−3x+1.
(3)-2x³+1(答案不唯一)
查看更多完整答案,请扫码查看


