《2025年行知天下九年级数学上册青岛版》

4. 某市举行足球邀请赛，规定参赛的每两个队之间比赛一场，共安排了 60 场比赛.设比赛组织者邀请了$x$个队参赛，则下列方程正确的是(D).

A.$\frac{1}{2}x(x + 1) = 60$
B.$x(x - 1) = 60$
C.$x(x + 1) = 60$
D.$\frac{1}{2}x(x - 1) = 60$

答案： 4.D

5. 某机械厂七月份生产零件 100 万个，第三季度生产零件 392 万个.设该厂八、九月份平均每月的增长率为$x$，那么$x$满足的方程是(D).

A.$100(1 + x)^2 = 392$
B.$100 + 100(1 + x)^2 = 392$
C.$100 + 100(1 + x) + 100(1 + 2x) = 392$
D.$100 + 100(1 + x) + 100(1 + x)^2 = 392$

答案： 5.D

6. 某种产品预计两年内成本将下降 36％，则年平均下降率为20％.

答案： 6.20％

7. 将一块正方形铁皮的四角各剪去一个边长为 3 cm 的小正方形，做成一个无盖的盒子.已知盒子的容积为 300 $cm^3$，则原铁皮的边长为16cm.

答案： 7.16

8. 某商场将进货价为 45 元的某种服装以 65 元售出，平均每天可售 30 件，为了尽快减少库存，商场决定采取适当的降价措施，调查发现：每件降价 1 元，则每天可多售 5 件.如果每天要盈利 800 元，每件应降价10元.

答案： 8.10

9. 秋冬季节为流感的高发期，有一人患了流感，经过两轮传染后共有 121 人患了流感，每轮传染中平均一个人传染的人数为10.

答案： 9.10

10. 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数为 73，则每个支干长出8支小分支.

答案： 10.8

11. 如图，一农户要建一个矩形鸡舍，鸡舍的一边利用长为 12 m 的住房墙，另外三边用 25 m 长的建筑材料围成.为方便进出，在垂直于住房墙的一边留一个 1 m 宽的门.所围矩形鸡舍的长、宽分别为多少时，鸡舍面积为 80 $m^2$?

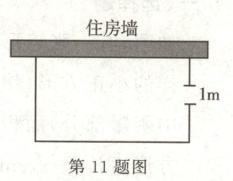
答案： 11.解：设矩形鸡舍垂直于住房墙一边长为$x$m，可以得出平行于墙的一边的长为$(25 - 2x + 1)$m.
由题意得$x(25 - 2x + 1) = 80$，
化简，得$x^{2} - 13x + 40 = 0$，
解得$x_{1} = 5$，$x_{2} = 8$.
当$x = 5$时，$26 - 2x = 16 ＞ 12$（舍去）；
当$x = 8$时，$26 - 2x = 10 ＜ 12$.
答：所围矩形鸡舍的长为$10$m、宽为$8$m.

12. 某市从 2020 年起连续投入资金用于“建设美丽城市，改造老旧小区”.已知每年投入资金的增长率相同，其中 2020 年投入资金 1000 万元，2022 年投入资金 1440 万元.
(1)求该市改造老旧小区投入资金的年平均增长率.
(2)2022 年老旧小区改造的平均费用为每个 80 万元，2023 年为提高老旧小区品质，每个小区改造费用计划增加 20％.如果投入资金年增长率保持不变，求该市 2023 年最多可以改造多少个老旧小区.

答案： 12.解：
(1)设该市改造老旧小区投入资金的年平均增长率为$x$.
依题意得$1000(1 + x)^{2} = 1440$，
解得$x_{1} = 0.2 = 20\%$，$x_{2} = - 2.2$（不合题意，舍去）.
答：该市改造老旧小区投入资金的年平均增长率为$20\%$.
(2)设该市在2023年可以改造$y$个老旧小区，
依题意得$80 × (1 + 20\%)y \leq 1440 × (1 + 20\%)$，
解得$y \leq 18$.
又因为$y$为整数，
所以$y$的最大值为$18$.
答：该市在2023年最多可以改造$18$个老旧小区.