第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
6. 如图,某零件的外径为$10 cm$,用一个交叉卡钳(两条尺长$AC$和$BD$相等)可测量零件的内孔直径$AB$.如果$OA : OC = OB : OD = 3$,且量得$CD = 3 cm$,则零件的厚度$x$为(

A.$0.3 cm$
B.$0.5 cm$
C.$0.7 cm$
D.$1 cm$
B
).
A.$0.3 cm$
B.$0.5 cm$
C.$0.7 cm$
D.$1 cm$
答案:
6.B
7. 如图,在$\triangle ABC$中,$D$,$E$分别是边$BA$,$CA$延长线上的点,且$DE // BC$.如果$\frac{DE}{BC} = \frac{3}{5}$,$CE = 4$,那么$AE$的长为
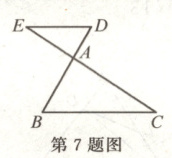
$\frac{3}{2}$
.
答案:
7.$\frac{3}{2}$
8. 如图,已知有两堵墙$AB$,$CD$,墙$AB$高$2$米,两墙之间的距离$BD$为$8$米,小明将一架木梯放在距$B$点$3$米的$P$处靠向墙$AB$时,木梯有很多露出墙外,将木梯绕点$P$旋转$90^{\circ}$靠向墙$CD$时,木梯刚好达到墙$CD$的顶端,则墙$CD$的高为
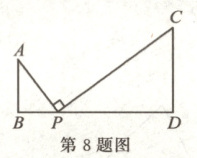
7.5米
.
答案:
8.7.5米
9. 如图所示,$\angle ABC = \angle D = 90^{\circ}$,$AC = 5$,$BC = 4$,当$BD =$

$\frac{12}{5}$或$\frac{16}{5}$
时,图中两直角三角形相似.
答案:
9.$\frac{12}{5}$或$\frac{16}{5}$
10. 如图,点$D$,$E$分别在$\triangle ABC$的$AB$,$AC$边上.只需添加一个条件即可证明$\triangle AED \backsim \triangle ACB$,这个条件可以是
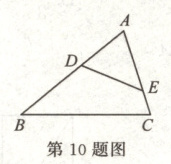
∠ADE = ∠C(答案不唯一)
.(写出一个即可)
答案:
10.∠ADE = ∠C(答案不唯一)
11. 如图,在$\triangle ABC$中,$BC$的垂直平分线$MN$交$AB$于点$D$,$CD$平分$\angle ACB$.若$AD = 2$,$BD = 3$,则$AC$的长
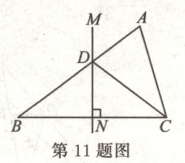
$\sqrt{10}$
.
答案:
11.$\sqrt{10}$
12. 希腊数学家海伦给出了挖掘直线隧道的方法:如图,$A$,$B$是两侧山脚的入口,从$B$出发任意作线段$BC$,过$C$作$CD \perp BC$,然后依次作垂线段$DE$,$EF$,$FG$,$GH$,直到接近$A$点,作$AJ \perp GH$于点$J$.每条线段可测量,长度如图所示.分别在$BC$,$AJ$上任选点$M$,$N$,作$MQ \perp BC$,$NP \perp AJ$,使得$\frac{PN}{AN} = \frac{QM}{BM} = k$,此时点$P$,$A$,$B$,$Q$共线.挖隧道时始终能看见$P$,$Q$处的标志即可.
(1)$CD - EF - GJ =$
(2)$k =$
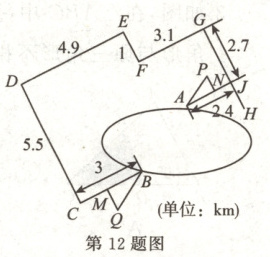
(1)$CD - EF - GJ =$
1.8
$ km$;(2)$k =$
$\frac{9}{13}$
.
答案:
12.1.8 $\frac{9}{13}$
13. 如图,在$\triangle ABC$中,$AB = 8$,$BC = 4$,$CA = 6$,$CD // AB$,$BD$是$\angle ABC$的平分线,$BD$交$AC$于点$E$.
(1)求证:$BC = CD$;
(2)求$AE$的长.
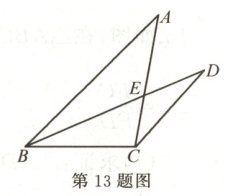
(1)求证:$BC = CD$;
(2)求$AE$的长.

答案:
13.
(1)证明:因为BD是∠ABC的平分线,
所以∠ABD = ∠DBC.
因为CD//AB,所以∠ABD = ∠BDC,
所以∠DBC = ∠BDC,
所以BC = CD.
(2)解:因为CD//AB,所以△ABE∽△CDE,
所以$\frac{AE}{CE}$ = $\frac{AB}{CD}$.
因为AB = 8,CD = BC = 4,所以$\frac{AE}{CE}$ = $\frac{8}{4}$.
因为AE = 2CE,
又因为AE + CE = AC = 6,所以AE = 4.
(1)证明:因为BD是∠ABC的平分线,
所以∠ABD = ∠DBC.
因为CD//AB,所以∠ABD = ∠BDC,
所以∠DBC = ∠BDC,
所以BC = CD.
(2)解:因为CD//AB,所以△ABE∽△CDE,
所以$\frac{AE}{CE}$ = $\frac{AB}{CD}$.
因为AB = 8,CD = BC = 4,所以$\frac{AE}{CE}$ = $\frac{8}{4}$.
因为AE = 2CE,
又因为AE + CE = AC = 6,所以AE = 4.
查看更多完整答案,请扫码查看


