第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
3.山西老陈醋是中国四大名醋之一,已有$3000$余年的历史,素有“天下第一醋”的盛誉,以色、香、醇、浓、酸五大特征著称于世.某工厂$2021$年老陈醋的产量为$5$万吨,随着引进新技术,$2023$年的产量预计能达到$7.2$万吨,设年平均增长率为$x$,则可列方程为(
A.$5(1 - x)^{2}=7.2$
B.$5(1 + x)^{2}=7.2$
C.$5(1 + 2x)=7.2$
D.$5(2 + x)=7.2$
B
).A.$5(1 - x)^{2}=7.2$
B.$5(1 + x)^{2}=7.2$
C.$5(1 + 2x)=7.2$
D.$5(2 + x)=7.2$
答案:
3.B
4.将代数式$x^{2}+4x - 1$化成$(x + h)^{2}+k$的形式为(
A.$(x - 2)^{2}+3$
B.$(x + 2)^{2}+4$
C.$(x + 2)^{2}-1$
D.$(x + 2)^{2}-5$
D
).A.$(x - 2)^{2}+3$
B.$(x + 2)^{2}+4$
C.$(x + 2)^{2}-1$
D.$(x + 2)^{2}-5$
答案:
4.D
5.关于$x$的一元二次方程$ax^{2}+bx + c = 0$,若$4a - 2b + c = 0$,则该方程必有一个根是(
A.$x = - 2$
B.$x = 2$
C.$x = -\frac{1}{2}$
D.$x = \frac{1}{2}$
A
).A.$x = - 2$
B.$x = 2$
C.$x = -\frac{1}{2}$
D.$x = \frac{1}{2}$
答案:
5.A
6.在关于$x$的一元二次方程$ax^{2}+bx + c = 0$中,若$a$与$c$异号,则方程(
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
A
).A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
答案:
6.A
7.如图,一块长为$a\ m$,宽为$b\ m$的长方形土地的周长为$18\ m$,面积为$14\ m^{2}$.现将该长方形土地的长、宽都增加$2\ m$,则扩建后的长方形土地的面积为(
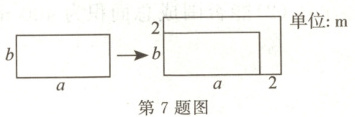
A.$32\ m^{2}$
B.$36\ m^{2}$
C.$27\ m^{2}$
D.$38\ m^{2}$
B
).
A.$32\ m^{2}$
B.$36\ m^{2}$
C.$27\ m^{2}$
D.$38\ m^{2}$
答案:
7.B
8.有两个人患了流行性感冒,经过两轮传染后,共有$392$人患了流行性感冒,则每轮传染中平均一个人传染的人数是(
A.$14$
B.$15$
C.$13$
D.$12$
C
).A.$14$
B.$15$
C.$13$
D.$12$
答案:
8.C
9.方程$x(x + 3)=4(x + 3)$的解是
-3或4
.
答案:
9.-3或4
10.若关于$x$的方程$(a - 2)x^{|4 - a|}+7x - 1 = 0$是一元二次方程,则$a$的值为
6
.
答案:
10.6
11.小明用配方法解一元二次方程$x^{2}-6x + 5 = 0$,将它化成$(x - p)^{2}=q$的形式,则$p + q$的值为
7
.
答案:
11.7
12.若$x = 2$是关于$x$的方程$ax^{2}-bx = 2$的解,则$2023 - 6a + 3b$的值为
2020
.
答案:
12.2020
13.对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$,下列说法:
①若$c$是方程$ax^{2}+bx + c = 0$的一个根,则一定有$ac + b + 1 = 0$成立;
②若方程$ax^{2}+c = 0$有两个不相等的实根,则方程$ax^{2}+bx + c = 0$必有两个不相等的实根;
③若$a - b + c = 0$,则它有一根为$-1$;
④若$b = 2a + 3c$,则一元二次方程$ax^{2}+bx + c = 0$有两个不相等的实数根.
其中正确的为
①若$c$是方程$ax^{2}+bx + c = 0$的一个根,则一定有$ac + b + 1 = 0$成立;
②若方程$ax^{2}+c = 0$有两个不相等的实根,则方程$ax^{2}+bx + c = 0$必有两个不相等的实根;
③若$a - b + c = 0$,则它有一根为$-1$;
④若$b = 2a + 3c$,则一元二次方程$ax^{2}+bx + c = 0$有两个不相等的实数根.
其中正确的为
②③④
.
答案:
13.②③④
查看更多完整答案,请扫码查看


