《2025年行知天下九年级数学上册青岛版》

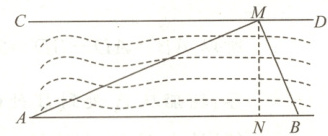
例题1 小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的河流宽度.
他先在河岸设立$A$，$B$两个观测点，然后选定对岸河边的一棵树记为点$M$，测得$AB = 50 m$，$\angle MAB = 22^{\circ}$，$\angle MBA = 67^{\circ}$.请你依据所测数据，求出这段河流的宽度(结果精确到$0.1 m$).

参考数据：$\sin22^{\circ} \approx \frac{3}{8}$，$\cos22^{\circ} \approx \frac{15}{16}$，
$\tan22^{\circ} \approx \frac{2}{5}$，$\sin67^{\circ} \approx \frac{12}{13}$，$\cos67^{\circ} \approx \frac{5}{13}$，$\tan67^{\circ} \approx \frac{12}{5}$.

答案： 分析：过点$M$作$MN \perp AB$，垂足为$N$，设$MN = x$米，分别在$ Rt \triangle ANM$和$ Rt \triangle MNB$中，利用锐角三角函数的定义求出$AN$，$BN$的长，然后根据$AB = 50$米，列出关于$x$的方程，进行计算即可解答.
解：过点$M$作$MN \perp AB$，垂足为$N$.设$MN = x$米，
在$ Rt \triangle ANM$中，$\angle MAB = 22^{\circ}$，所以$AN = \frac{MN}{\tan22^{\circ}} \approx \frac{x}{\frac{2}{5}} = \frac{5}{2}x( 米)$.
在$ Rt \triangle MNB$中，$\angle MBN = 67^{\circ}$，所以$BN = \frac{MN}{\tan67^{\circ}} \approx \frac{x}{\frac{12}{5}} = \frac{5}{12}x( 米)$.
因为$AB = 50$米，所以$AN + BN = 50$，所以$\frac{5}{2}x + \frac{5}{12}x = 50$，所以$x \approx 17.1$，
所以这段河流的宽度约为$17.1$米.
点拨：本题考查了解直角三角形的应用——仰角俯角问题.根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.

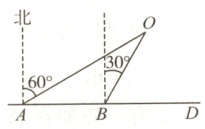
例题2 如图，某轮船在海上向正东方向航行，上午$8:00$在点$A$处测得小岛$O$在北偏东$60^{\circ}$方向的$16\sqrt{3} km$处，上午$8:30$轮船到达$B$处，测得小岛$O$在北偏东$30^{\circ}$方向.
(1)求轮船从$A$处到$B$处的航速；
(2)如果轮船按原速继续向东航行，还需经过多少时间轮船才恰好位于小岛的东南方向？

答案：
分析：
(1)过点$O$作$OD \perp AB$，垂足为$D$，构造直角三角形，利用特殊角的三角函数值先求出$AB$，再利用路程、速度和时间之间的关系求出轮船的航速.
(2)过点$O$作$\angle DOE = 45^{\circ}$交$AD$的延长线于点$E$.求出$BE$的长，再求轮船航行的时间.
解：
(1)如图，过点$O$作$OD \perp AB$，垂足为$D$.
由题意知$\angle OAD = 30^{\circ}$，$\angle OBD = 60^{\circ}$.
在$ Rt \triangle OAD$中，因为$OA = 16\sqrt{3}$，$\angle OAD = 30^{\circ}$，
所以$OD = 8\sqrt{3}$，$AD = 24$.
在$ Rt \triangle OBD$中，因为$OD = 8\sqrt{3}$，$\angle OBD = 60^{\circ}$，
所以$BD = \frac{OD}{\tan60^{\circ}} = \frac{8\sqrt{3}}{\sqrt{3}} = 8$，
所以$AB = AD - BD = 24 - 8 = 16( km)$，所以$v = \frac{16}{0.5} = 32( km/h)$.
答：轮船从$A$处到$B$处的航速为$32 km/h$.
(2)过点$O$作$\angle DOE = 45^{\circ}$交$AD$的延长线于点$E$.
因为$\angle DOE = 45^{\circ}$，$\angle ODE = 90^{\circ}$，
所以$DE = OD = 8\sqrt{3} km$，$BE = BD + DE = 8 + 8\sqrt{3}( km)$，
所以$\frac{8 + 8\sqrt{3}}{32} = \frac{1 + \sqrt{3}}{4}( h)$.
答：轮船按原速继续向东航行，还需要航行$\frac{1 + \sqrt{3}}{4}$小时才恰好位于小岛的东南方向.
点拨：本题运用建模思想和数形结合思想解题，其解答的关键是构造直角三角形及解直角三角形.