《2025年同步学习目标与检测九年级数学全一册人教版》

1. 已知 $\odot O$ 的半径 $r = 5\ cm$,圆心到直线 $l$ 的距离 $OM = 4\ cm$,在直线 $l$ 上有一点 $P$,且 $PM = 3\ cm$,则点 $P$( )

A.在 $\odot O$ 内
B.在 $\odot O$ 上
C.在 $\odot O$ 外
D.可能在 $\odot O$ 上或在 $\odot O$ 内

答案： B

2. 下列各数中,可以用来说明命题“任何偶数都是 $4$ 的倍数”是假命题的反例是( )

A.$5$
B.$12$
C.$14$
D.$8$

答案： C

3. 有一题目：“已知点 $O$ 为 $\triangle ABC$ 的外心,$\angle BOC = 130^{\circ}$,求 $\angle A$。”嘉嘉的解答为：画 $\triangle ABC$ 以及它的外接圆 $O$,连接 $OB$,$OC$,如图。由 $\angle BOC = 2\angle A = 130^{\circ}$,得 $\angle A = 65^{\circ}$。而淇淇说：“嘉嘉考虑的不周全,$\angle A$ 还应有另一个不同的值。”下列判断正确的是( )


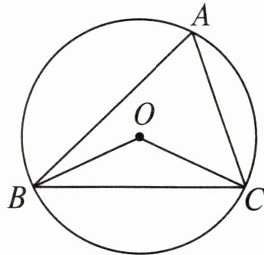
A.淇淇说的对,且 $\angle A$ 的另一个值是 $115^{\circ}$
B.淇淇说的不对,$\angle A$ 就得 $65^{\circ}$
C.嘉嘉求的结果不对,$\angle A$ 应得 $50^{\circ}$
D.两人都不对,$\angle A$ 应有 $3$ 个不同的值

答案： A

4. 在公园的 $O$ 处附近有 $E$,$F$,$G$,$H$ 四棵树,位置如图所示(图中小正方形的边长均相等)。现计划修建一座以 $O$ 为圆心,$OA$ 为半径的圆形水池,要求池中不留树木,则 $E$,$F$,$G$,$H$ 四棵树中需要被移除的为( )

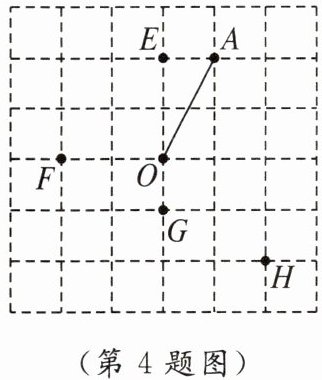
A.$E$,$F$,$G$
B.$F$,$G$,$H$
C.$G$,$H$,$E$
D.$H$,$E$,$F$

答案： A
∵OA=√(1²+2²)=√5，
∴OE=2＜OA，点E在⊙O内，
OF=2＜OA，点F在⊙O内，
OG=1＜OA，点G在⊙O内，
OH=√(2²+2²)=2√2＞OA，点H在⊙O外.
∴E，F，G三棵树需要被移除.

5. 如图,已知 $\triangle ABC$ 外接圆的直径为 $4$,$\angle ABC = 120^{\circ}$,则 $AC$ 的长为( )

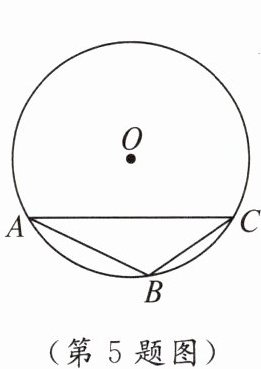
A.$2$
B.$2\sqrt{3}$
C.$4$
D.$4\sqrt{3}$

答案： B 如图所示，在弦AC所对的优弧上取一点D，连接DA，DC，OA，OC，作OH⊥AC，垂足为H.
∵四边形ABCD是圆内接四边形，
∴∠D=180°-120°=60°.
由圆周角定理，得∠AOC=120°.
∴∠OAC=∠OCA=30°，
∴AH=√3.
∴AC=2AH=2√3.

6. 已知 $\odot O$ 的半径为 $4$,点 $P$ 与圆心 $O$ 的距离为 $d$,且方程 $x^{2} - 4x + d = 0$ 有实数根,则点 $P$ 在 $\odot O$____。(填位置关系)

答案： 内或上
∵方程x²-4x+d=0有实数根，
∴Δ=b²-4ac=16-4d≥0，
∴d≤4，
∴d≤r.
当d＜r时，点P在⊙O内；当d=r时，点P在⊙O上.
∴点P在⊙O的内部或点P在⊙O上.

7. ①直径是弦,②经过三点一定可以作圆,③三角形的外心到三角形各顶点的距离相等,④长度相等的弧是等弧,⑤平分弦的直径垂直于弦。以上说法中正确的是____(填序号)。

答案： ①③ 直径是弦，所以①正确；经过不共线的三点一定可以作圆，所以②错误；三角形的外心到三角形各顶点的距离相等，所以③正确；能够完全重合的弧是等弧，所以④错误；平分弦(非直径)的直径垂直于弦，所以⑤错误.故答案为①③.

8. 如图,在边长为 $1$ 的正方形网格中,$\triangle ABC$ 的顶点均在格点上,点 $A$,$B$ 的坐标分别是 $A(5,3)$,$B(5,1)$。在图中标出 $\triangle ABC$ 外心 $D$ 的位置,并直接写出它的坐标。

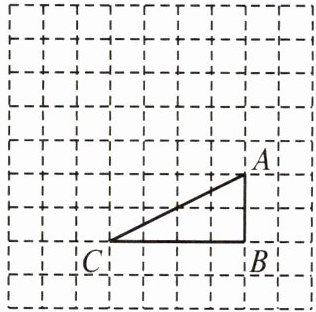
答案： 解：如图，
△ABC的外心D点的坐标为(3,2).