《2025年同步学习目标与检测九年级数学全一册人教版》

1. 某班同学毕业时都将自己的照片向全班其他同学各送一张留念,全班共送1980张照片,如果全班有 $ x $ 名同学,根据题意,列出方程为( )

A.$ x(x + 1) = 1980 $
B.$ x(x - 1) = 1980 $
C.$ \frac{1}{2}x(x + 1) = 1980 $
D.$ \frac{1}{2}x(x - 1) = 1980 $

答案： B

2. 某种商品的零售价经过两次降价后的价格为降价前的81%,则平均每次降价( )

A.10%
B.19%
C.9.5%
D.20%

答案： A 设平均每次降价$x$,由题意得$(1-x)^{2}=81\%$,解得$x_{1}=0.1=10\%$,$x_{2}=-1.9$(舍去).

3. 某种童鞋原价为100元,由于店面转让要清仓,经过连续两次降价处理,现以64元销售。已知两次降价的百分率相同,则每次降价的百分率为( )

A.19%
B.20%
C.21%
D.22%

答案： B

4. 某超市1月份的营业额为200万元,已知第一季度的总营业额为1000万元,如果平均每月营业额的增长率为 $ x $,那么由题意列方程应为( )

A.$ 200(1 + x)^2 = 1000 $
B.$ 200 + 200×2x = 1000 $
C.$ 200 + 200×3x = 1000 $
D.$ 200[1 + (1 + x) + (1 + x)^2] = 1000 $

答案： D 因为1月份的营业额为200万元,2月份的营业额增长了$200x$万元,所以2月份的营业额为$200+200x=200(1+x)$(万元);3月份的营业额在2月份的基础上增长了$200(1+x)x$万元,达到$200(1+x)+200(1+x)x=200(1+x)^{2}$(万元).
因此第一季度总营业额为$[200+200(1+x)+200(1+x)^{2}]$万元,即$200[1+(1+x)+(1+x)^{2}]$万元.

5. 有一人患了流感,经过两轮传染后,共有121人患了流感,每轮传染中平均每人传染了______人。

答案： 10 设每轮传染中平均每人传染了$x$人.
依题意,得$1+x+x(1+x)=121$,即$(1+x)^{2}=121$,解方程,得$x_{1}=10$,$x_{2}=-12$(舍去).
故每轮传染中平均每人传染了10人.

6. 若一个两位数等于它的个位上的数的平方,且个位上的数比十位上的数大3,则这个两位数为______。

答案： 25或36 设这个两位数的个位数字为$x$,则十位数字应该是$x-3$,由题意,得$10(x-3)+x=x^{2}$,解得$x_{1}=5$,$x_{2}=6$.故这个两位数是25或36.

7. 去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为450万元,第七天的营业额是前六天总营业额的12%。
(1) 求该商店去年“十一黄金周”这七天的总营业额；
(2) 去年该商站7月份的营业额为350万元,8、9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份营业额相等,求该商店去年8、9月份营业额的月增长率。

答案： 解:
(1)$450+450×120\%=504$(万元).
答:该商店去年"十一黄金周"这七天的总营业额为504万元.
(2)设该商店去年8、9月份营业额的月增长率为$x$.
依题意,得$350(1+x)^{2}=504$,解得$x_{1}=0.2=20\%$,$x_{2}=-2.2$(不合题意,舍去).
答:设该商店去年8、9月份营业额的月增长率为20%.

8. 某旅行社为吸引市民组团去甲风景区旅游,推出了如下收费标准：

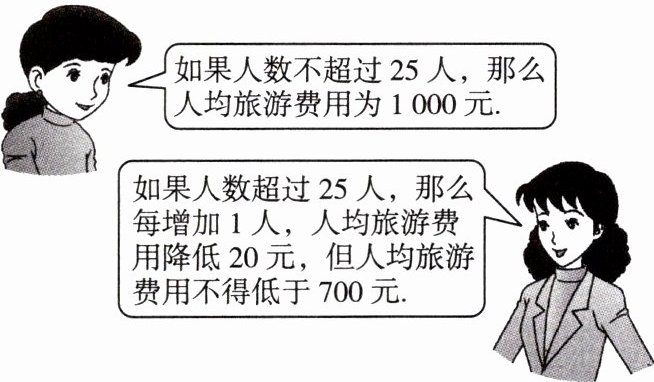
某单位组织员工去甲风景区旅游,共支付给旅行社旅游费用27000元。请问该单位这次共有多少员工去甲风景区旅游？

答案： 解:设该单位这次共有$x$名员工去甲风景区旅游.
因为$1000×25=25000＜27000$.
所以员工人数一定超过25人,可得方程$[1000-20(x-25)]x=27000$.
整理,得$x^{2}-75x+1350=0$,解得$x_{1}=45$,$x_{2}=30$.
当$x_{1}=45$时,$1000-20(x-25)=600＜700$,故舍去$x_{1}$;
当$x_{2}=30$时,$1000-20(x-25)=900＞700$,符合题意.
答:该单位这次共有30名员工去甲风景区旅游.