《2025年同步学习目标与检测九年级数学全一册人教版》

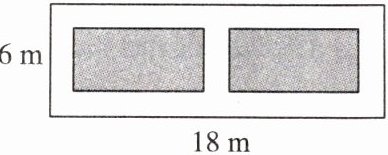
1.如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60$m^2$,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为xm,则可以列出关于x的方程是( )


A.$x^2+9x-8= 0$
B.$x^2-9x-8= 0$
C.$x^2-9x+8= 0$
D.$2x^2-9x+8= 0$

答案： C

知识点二 商品利润问题
【例2】某商品现在的售价为每件60元,每周可卖出300件.市场调查反映每降价1元,每周可多卖20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将售价定为多少元？
思路点拨(1)若设每件降价x元,则每件售价为(60－x)元,每件的利润为(60－x－40)元.
(2)每件降价x元,每星期可多卖20x件,则每星期的销量为(300＋20x)件,再由总利润为6080元可列方程(60－x－40)(300＋20x)＝6080.
听课笔记：

答案： 设每件商品降价$x$元。
原售价为每件60元，降价后售价为$(60 - x)$元。
原进价为每件40元，降价后每件利润为$(60 - x - 40)$元。
原每周销量为300件，降价后每周销量为$(300 + 20x)$件。
根据总利润$=$每件利润$×$销售数量，可列方程：
$(60 - x - 40)(300 + 20x) = 6080$
$(20 - x)(300 + 20x) = 6080$
$6000+400x-300x-20x^2=6080$
$-20x^2 + 100x - 80 = 0$
$x^2 - 5x + 4 = 0$
$(x - 1)(x - 4) = 0$
解得：$x_{1} = 1$，$x_{2} = 4$。
由于题目要求顾客得实惠，即售价要尽可能低，因此选择降价更多的$x = 4$。
所以，售价应为$60 - 4 = 56(元)$。
答：应将售价定为56元。

2.某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元,为了尽快减少库存,商场决定采取适当的降价措施.调查发现,如果这种贺年卡每降价0.1元,那么商场平均每天可多售出100张.商场要想平均每天盈利120元,每张贺年卡应降价多少元？

答案： 解：设每张贺年卡应降价 $x$ 元，则 $(0.3-x)\left(500+\dfrac{100x}{0.1}\right)=120$，解得 $x=0.1$ 或 $x=-0.3$（舍去）.答：每张贺年卡应降价0.1元.

1.某校准备修建一个面积为180$m^2$的矩形活动场地,它的长比宽多11m,设场地的宽为xm,则可列方程为( )

A.$x(x-11)= 180$
B.$2x+2(x-11)= 180$
C.$x(x+11)= 180$
D.$2x+2(x+11)= 180$

答案： C

2.如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同的小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600$cm^2$,设剪去小正方形的边长为xcm,则可列方程为( )


A.$(30-2x)(40-x)= 600$
B.$(30-x)(40-x)= 600$
C.$(30-x)(40-2x)= 600$
D.$(30-2x)(40-2x)= 600$

答案： D

(第3题图)
3.如图,矩形ABCD的面积是15,边AB的长比AD的长大2,则AD的长是______.

答案： 3