《2025年同步学习目标与检测九年级数学全一册人教版》

1. 某商店经营一种玩具,已知所获利润y(单位：元)与销售的单价x(单位：元)之间的关系为$y= -x^2+24x+2956,$则获利最多为( )

A.3144元
B.3100元
C.144元
D.2956元

答案： B

2. 如图,假设篱笆(虚线部分)的长度为16m,则所围成矩形ABCD的最大面积是( )

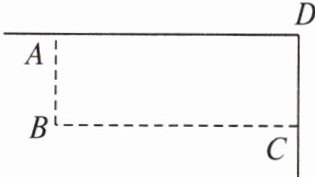
$A. 60m^2$
$B. 63m^2$
$C. 64m^2$
$D. 66m^2$

答案： C

3. 出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,则当x= ______元时,一天出售该种手工艺品的总利润y最大.

答案： 4

4. 某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(单位：m),占地面积为y(单位：$m^2).$如图,当饲养室的占地面积y最大时,饲养室长x= _________m.

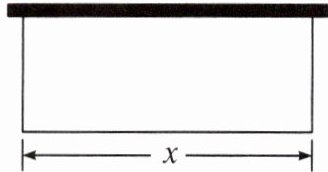
答案： 25

1. 已知某商品的销售利润y(单位：元)与该商品销售单价x(单位：元)之间满足$y= -20x^2+1400x-20000,$则获利最多为( )元.

A.4500
B.5500
C.450
D.20000

答案： A

2. 如图,用长8m的铝合金条制成如图形状的矩形窗框,使窗户的透光面积最大,则这个窗户的最大透光面积是( )


A.$\frac{64}{25}$m^2
B.$\frac{4}{3}$m^2
C.$\frac{8}{3}$m^2
$D.4m^2$

答案： C

3. 生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的月利润y和月份n之间的函数解析式为$y= -n^2+14n-24,$则该企业一年中应停产的月份是( )

A.1月,2月,3月
B.2月,3月,4月
C.1月,2月,12月
D.1月,11月,12月

答案： C

4. 用一条长为40cm的绳子围成一个面积为$a cm^2$的长方形,则a的值不可能为( )

A.20
B.40
C.100
D.120

答案： D

5. 若一个三角形的底边和底边上的高的和为10,则这个三角形的面积最大为______.

答案： 12.5

6. 某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现：每降价1元,每月可多售出20顶,已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为______.

答案： 70

7. 某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量y(单位：万件)与销售单价x(单位：元)之间的关系可以近似地看作一次函数y= -2x+100.
(1)写出每月的利润L(单位：万元)与销售单价x(单位：元)之间的函数关系式；
(2)当销售单价为多少元时,厂商每月能获得312万元的利润? 当销售单价为多少元时,厂商每月能获得最大利润? 最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?

答案： 解:
(1)L=(x-18)y=(x-18)(-2x+100)=-2x²+136x-1800,故L与x之间的函数关系式为L=-2x²+136x-1800.
(2)由L=312,得312=-2x²+136x-1800,解这个方程得x₁=24,x₂=44,所以销售单价定为24元或44元,厂商每月能获得312万元的利润.将L=-2x²+136x-1800配方,得L=-2(x-34)²+512,因此,当销售单价为34元时,每月能获得最大利润,最大利润是512万元.
(3)结合
(2)及函数L=-2x²+136x-1800的图象可知,当24≤x≤44时,L≥312,又由限价32元,得24≤x≤32,根据一次函数的性质,得y=-2x+100中y随x的增大而减小,故当x=32时,每月制造成本最低,最低成本是18×(-2×32+100)=648(万元),因此,所求每月最低制造成本为648万元.