《2025年同步学习目标与检测九年级数学全一册人教版》

4. 在某一电路中,保持电压不变,电流I(单位：A)与电阻R(单位：$ \Omega $)成反比例,当电阻$ R = 5\Omega $时,电流$ I = 2A $。则I与R之间的函数解析式为______。

答案： $I=\frac{10}{R}$ 设$I=\frac{k}{R}(k\neq0)$，将$R=5$，$I=2$代入，得$k=IR=2×5=10$，所以$I$与$R$之间的函数解析式为$I=\frac{10}{R}$.

1. 某工厂现有原材料100t,每天平均用去xt,这批原材料能用y天,则y与x之间的函数解析式为( )

A.$ y = 100x $
B.$ y = \frac{100}{x} $
C.$ y = \frac{x}{2} + 100 $
D.$ y = 100 - x $

答案： B

2. 在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度$ \rho $也随之改变,$ \rho $与V在一定范围内满足$ \rho = \frac{m}{V} $,它的图象如图所示,则该气体的质量m为( )


A.1.4kg
B.5kg
C.7kg
D.6.4kg

答案： C
∵$\rho=\frac{m}{V}$，
∴$m=\rho V$，而点$(5,1.4)$在图象上，代入得$m=5×1.4=7(kg)$.

3. 在下列选项中的两个变量之间,是反比例函数关系的为( )

A.在直角三角形中,$ 30° $角所对的直角边y与斜边x之间的关系
B.在等腰三角形中,顶角y与底角x之间的关系
C.圆的面积S与它的直径d之间的关系
D.面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系

答案： D

4. 某蔬菜生产基地在气温较低时,在装有恒温系统的大棚中栽培一种在自然光照且温度为$ 18° C $的条件下生长最快的新品种。如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(单位：$ ° C $)随时间x(单位：h)变化的函数图象,其中BC段是双曲线$ y = \frac{k}{x} (k \neq 0) $的一部分,则当$ x = 16 $时,大棚内的温度约为( )


A.$ 18° C $
B.$ 15.5° C $
C.$ 13.5° C $
D.$ 12° C $

答案： C 因为点$B(12,18)$在双曲线$y=\frac{k}{x}$上，所以$18=\frac{k}{12}$，解得$k=216$.当$x=16$时，$y=\frac{216}{16}=13.5$.所以当$x=16$时，大棚内的温度约为$13.5\ °C$.

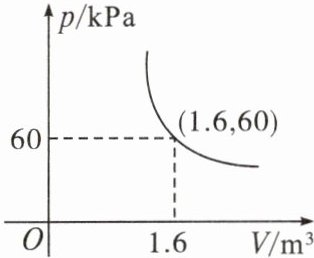
5. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位：kPa)与气体体积V(单位：$ m^3 $)成反比例函数关系,其图象如图。当气球内的气压大于120kPa时,气球将爆炸。为了安全起见,气球的体积应不小于______。

答案： $\frac{4}{5}\ m^3$ 设球内气体的气压$p$和气体体积$V$的解析式为$p=\frac{k}{V}(k\neq0)$.
∵图象过点$(1.6,60)$，
∴$k=96$，即$p=\frac{96}{V}$.函数$p$在第一象限内，$p$随$V$的增大而减小，
∴当$p\leqslant120$时，$V=\frac{96}{p}\geqslant\frac{4}{5}$.故答案为不小于$\frac{4}{5}\ m^3$.

6. 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地。为了安全、迅速地通过这片湿地,他们沿着前进路线铺了若干块木板。木板对地面的压强是木板面积的反比例函数,其图象如图所示。
(1)请直接写出这一函数解析式和自变量的取值范围；
(2)当木板面积为$ 3m^2 $时,压强是多少？
(3)如果要求压强不超过100Pa,那么木板的面积至少要多大？

答案： 解：
(1)设$p=\frac{k}{S}(k\neq0)$.把$A(1.5,400)$代入，得$400=\frac{k}{1.5}$，$k=1.5×400=600$，故$p=\frac{600}{S}(S＞0)$.
(2)当$S=3$时，$p=\frac{600}{3}=200$，即压强是$200\ Pa$.
(3)由题意知$\frac{600}{S}\leqslant100$，解得$S\geqslant6$.