《2025年同步学习目标与检测九年级数学全一册人教版》

1. 甲口袋中有1个红球和1个黄球,乙口袋中有1个红球、1个黄球和1个绿球,这些球除颜色外都相同.从两个口袋中各随机取一个球,取出的两个球都是红球的概率为( )

A.$\frac{1}{6}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{5}{6}$

答案： A

2. 如图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和是2的倍数或是3的倍数的概率等于( )


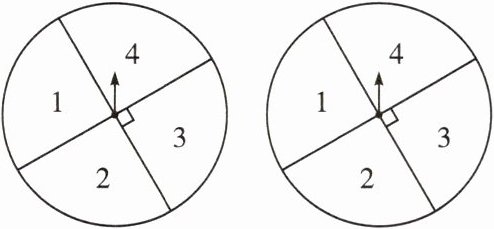
A.$\frac{3}{16}$
B.$\frac{3}{8}$
C.$\frac{5}{8}$
D.$\frac{13}{16}$

答案： C

3. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )

A.$\frac{1}{4}$
B.$\frac{2}{3}$
C.$\frac{1}{3}$
D.$\frac{3}{16}$

答案： C

4. 同时投掷三枚质地均匀的硬币,朝上的面都相同的概率为( )

A.$\frac{1}{3}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
D.$\frac{1}{8}$

答案： B

5. 如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )


A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{6}$

答案： A

6. 在一个不透明的袋子里有2个黑球和1个白球,除了颜色外其他全部相同,任意摸两个球,摸到1个黑球和1个白球的概率是______.

答案： $\frac{2}{3}$

7. 先从0,1,2这三个数中任取一个数作为点P的横坐标,再从剩下的两个数中任取一个数作为点P的纵坐标,则点P落在抛物线$y = -x^2 + x + 2$上的概率为______.

答案： $\frac{1}{2}$

8. 甲、乙、丙三名同学打乒乓球,想通过“手心手背”游戏来决定其中哪两人先打.规则如下：三人同时各用一只手随机出示手心或手背,若只有两人手势相同(都是手心或都是手背),则这两人先打；若三人手势相同,则重新决定.那么通过一次“手心手背”游戏能决定甲打乒乓球的概率是______.

答案： $\frac{1}{2}$

9. 甲、乙两人玩猜数字游戏,游戏规则如下：有四个数字0,1,2,3,先由甲心中任选一个数字,记为m,再由乙猜甲刚才所选的数字,记为n.若m,n满足$|m - n| \leq 1$,则称甲、乙两人“心有灵犀”.则甲、乙两人“心有灵犀”的概率是______.

答案： $\frac{5}{8}$

10. 不透明的袋中装有3个大小相同的小球,其中两个为白色,一个为红色,随机地从袋中摸取一个小球后放回,再随机地摸取一个小球.(用列表法或树状图求下列事件的概率)
(1)两次取的小球都是红球的概率；
(2)两次取的小球是一红一白的概率.

答案：
解:树状图如图.

(1)两次取的小球都是红球的概率为$\frac{1}{9}$.
(2)由树状图可得，两次取的小球是一红一白的有4种，故其概率为$\frac{4}{9}$.