《2025年同步学习目标与检测九年级数学全一册人教版》

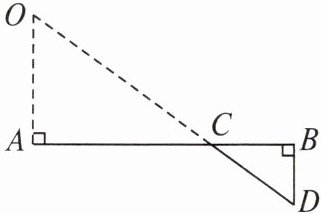
【例2】如图,为了测量一大峡谷的宽度,地质勘探人员在对面的岩石上观测到一个特别明显的标志点$O$,再在他们所在的这一侧选点$A$,$B$,$D$,使得$AB\perp AO$,$DB\perp AB$,然后确定$DO和AB的交点C$,测得$AC = 120 m$,$CB = 60 m$,$BD = 50 m$,你能帮他们算出峡谷的宽$AO$吗？

听课笔记：______

答案： 解：
∵AB⊥AO，DB⊥AB，
∴DB//OA.
∴△AOC∽△BDC.
∴$\frac{OA}{DB}=\frac{AC}{BC}$，即$\frac{OA}{50}=\frac{120}{60}$，解得OA=100(m).
答：峡谷的宽AO为100 m.

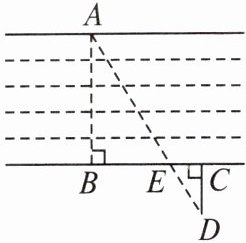
2. 为测量某河的宽度,小军先在河对岸选定一个目标点$A$,再在他所在的这一侧选点$B$,$C$,$D$,使得$AB\perp BC$,$CD\perp BC$,最后找出$AD与BC的交点E$.如图,若测得$BE = 90 m$,$EC = 45 m$,$CD = 60 m$,则这条河的宽$AB$等于( )


A.$120 m$
B.$67.5 m$
C.$40 m$
D.$30 m$

答案： A
∵AB⊥BC，CD⊥BC，
∴△BAE∽△CDE，
∴$\frac{AB}{CD}=\frac{BE}{CE}$.
∵BE=90 m，CE=45 m，CD=60 m，
∴$\frac{AB}{60}=\frac{90}{45}$，解得AB=120 m.

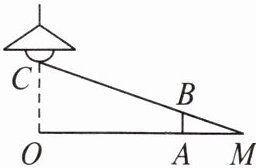
1. 如图,路灯距离地面$8 m$,身高$1.6 m$的小明站在距离灯的底部(点$O$)$20 m的A$处,则小明的影长为( )


A.$4 m$
B.$5 m$
C.$6 m$
D.$7 m$

答案： B 由题意可得OC//AB，则△MBA∽△MCO，故$\frac{CO}{AB}=\frac{OM}{AM}$，即$\frac{8}{1.6}=\frac{20 + AM}{AM}$，解得AM=5(m).

2. 已知网球单打比赛场地宽度为$8 m$,长度在球网的两侧各为$12 m$,球网高度为$0.9 m$(如图$AB$的高度).在比赛中,某运动员退出场地在距球网$14 m的D$点处接球,设计打出直线,使球落在对方底线上$C$处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点高度至少为( )


A.$1.65 m$
B.$1.75 m$
C.$1.85 m$
D.$1.95 m$

答案： D 由题意知AB//DE，
则△ABC∽△EDC，
∴$\frac{CB}{CD}=\frac{AB}{ED}$，即$\frac{12}{12 + 14}=\frac{0.9}{ED}$，解得ED=1.95(m).

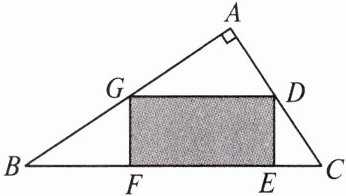
3. 如图,有一块直角三角形余料$ABC$,$\angle BAC = 90^{\circ}$,$D是AC$的中点,现从中切出一条矩形纸条$DEFG$,其中$E$,$F在BC$上,点$G在AB$上.若$BF = 4.5 cm$,$CE = 2 cm$,则纸条$GD$的长为( )


A.$3 cm$
B.$\frac{2}{13} cm$
C.$\frac{13}{2} cm$
D.$\frac{13}{3} cm$

答案： C 依题意得△AGD∽△ABC，
∴$\frac{GD}{BC}=\frac{AD}{AC}$，即$\frac{GD}{4.5 + GD + 2}=\frac{1}{2}$，解得GD=$\frac{13}{2}$(cm).

4. 如图,比例规是一种画图工具,它由长度相等的两脚$AD和BC$交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度$3$的地方(即同时使$OA = 3OD$,$OB = 3OC$),然后张开两脚,使$A$,$B两个尖端分别在线段l$的两个端点上,若$CD = 3.2 cm$,则$AB$的长为______$cm$.

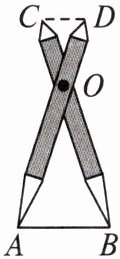
答案： 9.6
∵OA=3OD，OB=3CO，
∴OA:OD=BO:CO=3:1，∠AOB=∠DOC.
∴△AOB∽△DOC，
∴$\frac{AO}{OD}=\frac{AB}{CD}=\frac{3}{1}$，
∴AB=3CD.
∵CD=3.2 cm，
∴AB=9.6 cm.