《2025年名师面对面学科素养评价九年级数学全一册浙教版》

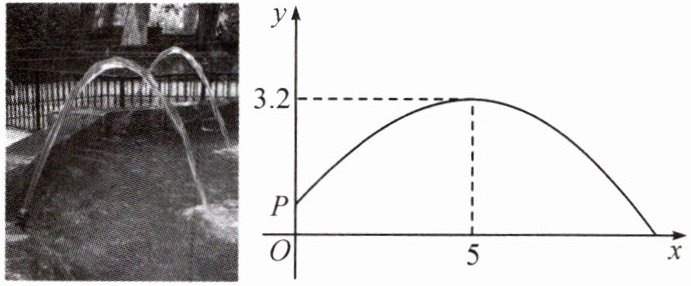
8. 小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头 $ P $ 距地面 $ 0.7 \, m $，水柱在距喷水头 $ P $ 水平距离 $ 5 \, m $ 处达到最高，最高点距地面 $ 3.2 \, m $. 建立如图所示的平面直角坐标系，并设抛物线的函数表达式为 $ y = a(x - h)^2 + k $，其中 $ x(m) $ 是水柱距喷水头的水平距离，$ y(m) $ 是水柱距地面的高度.
(1) 求抛物线的函数表达式.
(2) 爸爸站在水柱正下方，且距喷水头 $ P $ 水平距离 $ 3 \, m $. 身高 $ 1.6 \, m $ 的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离.

答案： 8.解:
(1)由图象可知抛物线顶点坐标为(5，3.2)，
　设抛物线的解析式为y=a(x−5)²+3.2,
　把点P(0,0.7)代入，解得a=−0.1,
∴抛物线的解析式为y=−0.1(x−5)²+3.2.
(2)小红身高1.6m,则1.6=−0.1(x−5)²+3.2,
　解得x₁=1或x₂=9,
∴小红距喷水头P水平距离1m或9m，
　即距离爸爸2m或6m.

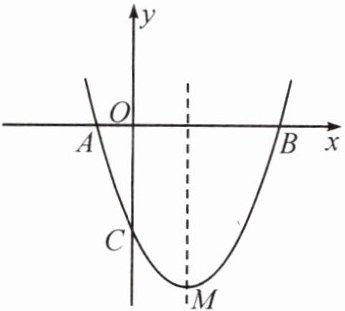
9. 如图所示，抛物线 $ y = x^2 - 2x - 3 $ 与 $ x $ 轴相交于 $ A $，$ B $ 两点，与 $ y $ 轴相交于点 $ C $，点 $ M $ 为抛物线的顶点.
(1) 求点 $ C $ 及顶点 $ M $ 的坐标.
(2) 若点 $ N $ 是第四象限内抛物线上的一个动点，连结 $ BN $，$ CN $，求 $ \triangle BCN $ 面积的最大值及此时点 $ N $ 的坐标.

答案：
9.解:
(1)C点坐标为(0，−3)，抛物线
　的顶点M的坐标为(1，−4).
(2)过N点作x轴的垂线交直线BC于Q点，连结BN,CN，由题意，得
B(3，0),A(−1,0),设直线BC的解析式为y=ax+b,代入C(0,−3)，
B(3,0),解得直线BC的解析式为y=x−3,设N点坐标为(n,n²−2n−3),
∴Q点坐标为(n,n−3),其中0＜n＜3，则S△BCN=S△NQC+S△NQB=$\frac{1}{2}$·QN·(xQ−xC)+$\frac{1}{2}$·QN·(xB−xQ)=$\frac{1}{2}$·QN·(xB−xC),且QN=(n−3)−(n²−2n−3)=−n²+3n,xB−xC=3,
∴S△BCN=$\frac{1}{2}$·(−n²+3n)·3=−$\frac{3}{2}$(n−$\frac{3}{2}$)²+$\frac{27}{8}$,其中0＜n＜3，当n=$\frac{3}{2}$时，S△BCN有最大值为$\frac{27}{8}$，此时点N的坐标为($\frac{3}{2}$,−$\frac{15}{4}$).